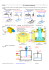12 Cor. 1: Tête à polir le marbre Sujet page 1 FIGURE DS.11: Tête à

12
Cor. 1: Tête à polir le marbre
Sujet page 1
Q1. Graphe des liaisons figure DS.11.
5
L56
L45
6
4
–
–
–
–
–
L61
L34
1
L13
3
L16
L13
L34
L45
L56
:
:
:
:
:
Liaison
Liaison
Liaison
Liaison
Liaison
(a) Graphe des liaisons
encastrement(par hypothèse) ;
pivot d’axe (O, #»
z ); ¡
¢
pivot glissant d’axe ¡O0 , #»
z ¢;
#»
0
pivot glissant
¡ d’axe
¢ O , y1 ,
pivot d’axe O, y#»
1 .
(b) Liaisons
F IGURE DS.11: Tête à polir
Q2. Hyperstatisme
On sait que m − h = Ic − Ec , d’où h = 1 avec
– Ic = 6 : le nombre d’inconnues cinématiques ;
– Ec = 6 · γ = 6 : le nombre d’équations issues de l’étude cinématique (avec γ = 1) ;
– m = 1 par hypothèse.
Q3. torseurs cinématiques


0
©
ª  0
0
0
V3/1 =


(O, z#»1 ¢)
γ31 0 ∀P∈
¡

©
ª  0
V(5/4 = β54

0

©
ª  0
0
V4/3 =

γ43
#» #» #»
? , ? ,z
1

0 
v 54

(O0 , y#»1¢)
0 ∀P∈
¡

©
ª  0
V6/5 = β65

0
#» #» #»
? ,y , ?
1
¡ #»
#Ȣ
#»
avec pour notation ? , y#»
1 , ? pour toute base comportant y 1 .
Q4. Fermeture cinématique
¡
#» #»¢
On choisit d’écrire la fermeture cinématique en O’ et dans la base x#»
1 , y 1 , z1 .
Changements depoint
 0
{V3/1 } = 0

γ31
Équations de fermeture

−e · γ31 · cos θ31 
−e · γ31 · sin θ31

0
O0
#» #»
( x#»
1 , y 1 , z1 )












0
0
γ31

−e·γ31 cos θ31






−e·γ31 sin θ31




0

 0
{V6/5 } = β65

0
+0
+0
+0
=0
+γ43
+0
+0
+0
+0
=0
+0
+v 54
+0
+0
+0
+0
+0
+0
#» #» #»
? ,y , ?
1
#» #»
( x#»
1 , y 1 , z1 )
+0
+β54
#» #» #»
? , ? ,z
1

0
0

(O, y#»1 ¢)
0 ∀P∈
¡

h · β65

0

e · β65 · sin θ31 O0
+0
+0

0 
0

(O0 , z#»1¢)
w 43 ∀P∈
¡
+β65
+h · β65
+e · β65 · sin θ31
+0
+0
+0
+0
+0
+0
+w 43
=0
=0
(DS.1)
=0
=0
Q5. Degré d’hyperstatisme
Le système ci-dessus comporte 6 équations et 6 inconnues, le rang est au maximum de 5 en effet la première équation (0 = 0) diminue le rang
de 1.

γ43 = −γ31




e
= γ31 cos θ31
Le rang du système est r c = 5. Pour résoudre ce système il faut poser 1 paramètre (ici il est judicieux de choisir γ31 ) et on obtient : β65

h



v 54
=γ31 sin θ31
(
β54
= −β65
puis
w 43 = −e · β65 · sin θ31
Le système est donc mobile d’ordre m = 1 (1 paramètre) et hyperstatique d’ordre h = 1 (h = Ec − r c ).
Q6. Modification de la liaison 3 – 4
Pour rendre le système isostatique, il faut ajouter une mobilité de rotation suivant x#»
1 afin de remplacer l’équation supplémentaire 0 = 0
13

0 
0
. Ce tor
w 43 O0
#»
#»
#»
( x¢1 , y 1 , z1 ) ©
¡
ª
seur ne correspond pas à une liaison normalisée mais se rapproche de la liaison sphère–cylindre de centre O’ et d’axe O0 , z#»
1 soit : V4/3 =


0 
α43
β
0

 43
γ43 w 43 O0
( x#»1 , y#»1 , z#»1 )
La fermeture géométrique devient :

©
ª α43
0
On nous propose de modifier la liaison 3 – 4 , rajoutons donc une mobilité, le torseur devient : V4/3 =

γ43


 α43 + 0




0 + β43




 0+0











+0 + 0
+0 + 0
+γ31 + γ43
0+0
−e · γ31 cos θ31 + 0
0+0
+0 + 0
0+0
−e · γ31 sin θ31 + 0
+0 + 0
+0 + 0
=0
+0 + 0
+0 + 0
=0
+β54 + β65
+0 + h · β65
+0 + 0
+0 + e · β65 · sin θ31
+0 + 0
+0 + 0
+v 54 + 0
+0 + w 43
=0
=0
(DS.2)
=0
=0
Le système à résoudre est un système 6 équations et 8 inconnues, le rang est de 6, le système est donc mobile d’ordre m = 2. La mobilité
¡ utile
¢
est inchangée, par contre une mobilité interne est rajoutée (équation β43 + β54 + β65 = 0), la rotation propre de la pièce 4 autour de l’axe O0 , y#»
1 .
14
Cor. 2: Changeur d’outil
Sujet page 2
A. Étude géométrique et cinématique
Q1. Établir le graphe de structure du module changeur et déterminer le nombre et la composition des cycles indépendants.
Pivot
(B, x#»
1)
6
γ = L − N + 1 = 2 soit deux cycles indépendants
Cycle 1 {1, 2, 3, 4}
Cycle 2 {1, 4 , 6, 5}.
4
Pivot
(D, x#»
1)
Liaison indéterminée
Pivot
(C, x#»
1)
5
Pivot
(E, x#»
1)
1
2
Pivot
(H, x#»
1)
3
Pivot
Glissant
(H, z#»
2)
Q2. Évaluer, par une analyse cinématique, le degré de mobilité de cette chaîne de mise en position. Calculer le degré d’hyperstaticité.
La boucle {1, 4 , 6, 5} est constituée de N = 4 solides, reliés par L = 4 liaisons pivots. On en déduit :
– γ = L − N + 1 = 1 boucle indépendante
– Ic = 4 × 1 = 4 inconnues cinématiques
– Ec = 6 × γ = 6 équations
Le rang du système ne peut être plus grand que r c < min(Ec , Ic ) = 4.
Ici, nous savons que le système est mobile et possède une seule mobilité m = 1. Nous pouvons en déduire le degré d’hyperstaticité m − h =
Ic − Ec soit h = 3.
Q3. Préciser le mouvement autorisé par la liaison
Lo14 entre la biellette de transmission (4) et le support (1), et écrire au point C puis au point B,
n
l’expression littérale du torseur cinématique V4/1 caractérisant ce mouvement, en fonction de la dérivée temporelle de θ14 , et des grandeurs
caractéristiques du mécanisme.
# »
n
o ½Ω
#»¾
d θ14
4/1 = ω4/1 · x 1
avec ω4/1 =
Rotation d’axe (C, x#»
#
» #»
1 ) soit : avec V4/1 =
VC∈4/1 = 0
dt
C
¾
¾
½ # »
# »
n
o ½
Ω4/1 = ω4/1 · x#»
Ω4/1 = ω4/1 · x#»
1
1
en B le torseur s’écrit : V4/1 = #
»
»
#» = #
#»
#»
VB∈4/1 = −b · ω4/1 · z 4 B
VB∈4/1 = ω4/1 · x 1 ∧ CB B
Q4. Préciser le mouvement autorisé par la liaison
n
oL15 entre la biellette d’orientation (5) et le support (1), et écrire au point E puis au point D,
l’expression littérale du torseur cinématique V5/1 caractérisant ce mouvement, en fonction de la dérivée temporelle de θ15 et des grandeurs
caractéristiques du mécanisme.
# »
n
o ½Ω
#»¾
d θ15
4/1 = ω5/1 · x 1
Rotation d’axe (E, x#»
avec ω5/1 =
#»
1 ) soit : V5/1 =
0
dt
C
¾
¾
½
# »
# »
n
o ½
Ω5/1 = ω5/1 · x#»
Ω5/1 = ω4/1 · x#»
1
1
en D ce torseur le torseur s’écrit : V5/1 = #
»
»
#» = #
#»
#»
VD∈5/1 = −b · ω5/1 · z 5 D
VD∈5/1 = ω5/1 · x 1 ∧ ED D
Q5. La figure constituée des points E, C, B et D est un parallélogramme. Sachant que dans un parallélogramme les cotés opposés restent parallèles(θ14 =
θ15 = δ), en déduire la nature du mouvement du porte-outil (6) par rapport au support (1). Comment est le champ des vecteurs vitesses de ce
mouvement ?
d δ #»
»
#
» #
Si θ14 = θ15 = δ alors VB∈4/1 = VD∈5/1 = −b ·
· z4
dt
Les points B et D sont les centres de deux liaisons pivots respectivement, entre le solide (6) et le solide (4) et entre le solide (6) et le solide (5).
d δ #» #
d δ #»
#
» #
» #
» #
»
» #
» #
» #
»
On peut déterminer VB∈6/1 = VB∈6/4 + VB∈4/1 = VB∈4/1 = b ·
· z 4 et VD∈6/1 = VD∈6/5 + VD∈5/1 = VD∈5/1 = b ·
· z 4 donc :
dt
dt
d δ #»
#
» #
»
· z4
VB∈6/1 = VD∈6/1 = −b ·
dt
Deux points du solide (6) ont même vitesse, le mouvement de (6) est donc une translation
n
o circulaire.
Q6. Écrire au point B puis au point P, l’expression littérale du torseur cinématique V6/1 caractérisant le mouvement du porte-outil (6) par
rapport au support (1) en fonction de la dérivée temporelle
deδ et des grandeurs caractéristiques du mécanisme.

#»
½
¾
½
¾
#»
#»

n
o 
0
0
0
Le solide (6) est en translation donc V6/1 =
=
=
d δ #»
#»
#»
−b ·
−b · ω51 · z 4 ∀P
−b · ω41 · z 4 ∀P
· z4 
dt
∀P
n
o
Q7. Écrire au point D puis au point E l’expression littérale du torseur cinématique V6/5 caractérisant le mouvement du porte-outil (6) par
rapport à la biellette d’orientation (5).
n
o n
o n
o
n
o ½
V6/5 = V6/1 + V1/5 en D cette égalité devient : V6/5 =
¾
½
¾
½# »
¾
½# »
¾
# »
Ω5/1 = ω51 · x#»
Ω6/5 = −ω51 · x#»
Ω6/5 = ω65 · x#»
0
1
1
1
− #
=
=
»
#»
#»
#»
#»
−b · ω51 · z 4 ∀P VD∈5/1 = −b · ω51 · z 4 D
0
0
D
D
¾
½# »
¾
½# »
# »
n
o ½Ω
#»¾
Ω6/5 = ω65 · x#»
Ω6/5 = −ω51 · x#»
6/5 = −ω51 · x 1
1
1
en E V6/5 =
=
=
# » #»
−b · ω51 · z#»
b · ω65 · z#»
Ω6/5 ∧ DE
4
4
E
E
E
#»
15
n
o
Q8. Écrire au point B puis au point E l’expression littérale du torseur cinématique V6/4 caractérisant le mouvement du porte-outil (6) par rapport
à la biellette de transmission (4). ½
¾
½# »
¾
# »
n
o
Ω6/4 = −ω41 · x#»
Ω6/4 = ω64 · x#»
1
1
De la même manière, V6/4 =
=
#»
#»
0
0
B
B
#»
#»
BE = e · y#»
on pose BE = f · y#»
1 − e · z 1 mais pour faciliter les calculs,
¡
¢4 + g · z 4 #»
#
» #
» # » # » #»
#»
#»
#»
#»
#»
VE∈6/4 = VB∈6/4 + Ω6/4 ∧ BE = 0 − ω41 · x 1 ∧ b · y 4 + f · y 4 + g · z 4 = −b · ω41 z 4 − f · ω41 z#»
4 + g · ω41 y 4
½
¾
¾
# »
# »
n
o ½
#»
Ω
=
Ω6/4 = −ω41 · x#»
1
6/4 ω64 · x 1
=
finalement le torseur s’écrit en E : V6/4 =
#»
#»
#»
#»
#»
#»
b · ω64 z 4 + f · ω64 z 4 − g · ω64 y 4 E
−b · ω41 z 4 − f · ω41 z 4 + g · ω41 y 4 E
Q9.nÉcrire
o fermeture cinématique de la chaîne de solide constituée des solides (1), (4), (5) et (6).
o liées
n à la
o n
o les
n six équations
V6/4 + V4/1 + V1/5 + V5/6 = {0}
n
o
On choisit d’écrire cette relation en E, il reste V4/1 à déplacer
½
¾
¾
# »
# »
n
o ½
Ω4/1 = ω41 · x#»
Ω
= ω41 · x#»
1
¡ 1#»
¢ = #
V4/1 = #
»
» 4/1
#»
#»
#»
#»
VE∈4/1 = ω41 · x 1 ∧ f · y 4 + g · z 4 E
VE∈4/1 = f · ω41 · z 4 − g · ω41 · y 4 E
½
½# »
½
¾
¾
¾
½# »
¾
# »
# »
Ω4/1 = ω41 · x#»
Ω5/1 = ω5/1 · x#»
Ω6/4 = ω64 · x#»
Ω6/5 = ω65 · x#»
1
1
1
1
+ #
−
= {0}
−
»
#»
#»
#»
#»
#»
#»
#»
b · ω64 z 4 + f · ω64 z 4 − g · ω64 y 4 E
b · ω65 · z 4
0
VE∈4/1 = f · ω41 · z 4 − g · ω41 · y 4 E
E
C
d’où les 6 équations de la fermeture cinématique :























ω64 + ω41 − ω51 − ω65 = 0
0 + 0 + 0 + 0+ = 0
0 + 0 + 0 + 0+ = 0
0 + 0 + 0 + 0+ = 0
−g · ω64 + g · ω41 + 0 + 0 = 0
b · ω64 + f · ω64 − f · ω41 − b · ω65 = 0
Q10. Déterminer le rang du système obtenu à la question précédente. En déduire le degré de mobilité et le degré d’hyperstatisme de la chaîne de
solide étudiée.
Le degré de mobilité est m = 1 (il faut fixer une des vitesse de rotation pour trouver les autres). Le rang est r c = 3 On déduit le degré d’hyperstaticité du nombre équations supplémentaires h = Ec − r c = 3
Q11. Proposer une modification permettant de rendre le mécanisme isostatique.
pour rendre le système isostatique, il faut ajouter dans une liaison pivot (ou plusieurs), un degré de liberté en translation suivant x#»
1 et deux
#»
rotations suivant z#»
1 et y 1 .
on peut donc :
– soit transformer une liaison pivot en Sphère Cylindre dont l’axe est suivant x#»
1,
– soit transformer une liaison pivot glissant et une autre en rotule.
Q12. Montrer, par une analyse cinématique que, si la liaison L34 est une liaison pivot d’axe (A, x#»
1 ), le degré d’hyperstaticité de la chaîne de mise
en mouvement n’est pas nul.
Pivot (A, x#»
1)
3
4
Pivot
Glissant(H, z#»
2)
Pivot (C, x#»
1)
1
Ic = 1 + 1 + 1 + 2 et Ec = 6 ;
Le sous mécanisme étudié comporte donc 6 équations avec 5 inconnues, le rang ne peut être supérieur au plus petit de Ec et Ic , il est
donc au maximum de r c ≤ 5.
On peut donc en déduire qu’il y a au moins Ec − r c = 1 équation
supplémentaire, le degré d’hypertatisme est donc h ≥ 1.
2
Pivot (H, x#»
1)
Q13. Dans le cas où la liaison L34 est une liaison rotule de centre A, calculer le degré de mobilité de la chaîne de mise en mouvement, et montrer
que ce système est isostatique. Identifier la (ou les) mobilité(s) de cette chaîne de mise en mouvement.
Sphérique de centre A
Ic = 1 + 1 + 3 + 2 = 7 et Ec = 6 ;
3
4
Pivot
Glissant(H, z#»
2)
Pivot (C, x#»
1)
1
2
Pivot (H, x#»
1)
Le sous mécanisme étudié comporte donc 6 équations avec 7 inconnues, le rang ne peut être supérieur au plus petit de Ec et Ic , il est
donc au maximum de r c ≤ 6.
Il est au moins mobile d’ordre m ≥ 1
On peut montrer que le mécanisme possède ici deux mobilités
– une mobilité utile m u = 1
– une mobilité interne m i = 1, la rotation de 3 autour de son axe
(A, x#»
2 ).
On peut alors écrire que m − h = Ic − Ec soit h = 0.
16
B. Détermination de l'eort développé par le vérin
support de l’action de 6→5
Équilibre de 5
Triangle des forces de 6
#
»
25mm = 50N
B4→6
57mm
#
»
D5→6
m
60 m
#»
P
Équilibre de 6
support de l’action de 3→ 4
#
»
75
#
m
m
50mm = 100 N
A3→4
»
C1→4
57mm
#
Triangle des forces de 4
»
B6→4
Equilibre de 4
Equilibre de 2-3
F IGURE DS.12: Équilibres de 4, 5, 6, 2-3
Q14. En isolant la biellette d’orientation (5), préciser sur le document réponse page 11 la direction de l’action mécanique en D du porte outil 6
sur la biellette 5, justifier et tracer sur le document réponse.
17
Soumise à 2 actions mécaniques, directement opposées (voir Équilibre de 5 sur la figure DS.12).
Q15. Préciser à combien d’action est soumis le porte outil (6), en déduire la direction et la norme de l’action en B de (4) sur (6), justifier et tracer
sur le document réponse.
le solide 6 est soumis à 3 actions mécaniques, ces 3 glisseurs sont concourants, On connaît
– la norme et la direction de l’action en P (50 N verticale)
– la direction de l’action en D (déterminée ci-dessus)
– le point d’application de la troisième est en B et passe par le point d’intersection des deux autres
(voir Équilibre de 6 sur la figure DS.12)
à partir de ces données, on trace le triangle des forces, en reportant les parallèles et en choisissant une échelle de représentation des forces, ici
25 mm=50 N.
Q16. Justifier que l’action en A de la biellette (4) sur la tige (2) est portée par la droite (A H), tracer sur le document réponse.
l’ensemble 2-3 est soumis à deux glisseurs qui sont directement opposés
Q17. En isolant maintenant la biellette de transmission (4), déterminer graphiquement la norme de l’action en A de la tige du vérin (2) sur la
biellette (4).
La biellette (4) est soumise à 3 glisseurs, on connaît :
– la norme et la direction de l’action en B (déterminée par l’équilibre de 6)
– la direction de l’action en A (déterminée par l’équilibre de 2-3)
– on deduit donc la direction de l’action en C
Le triangle des forces permet de résoudre complétement le problème, on obtient l’action en A de norme 100 N.