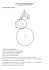Cercle d`Euler

Cercle d'Euler
Considérons le cercle
passant par les milieux
des cotés
Prenons M intersection
cercle et droite (BC)
B'C' // A'M
(réciproque Thalès)
La médiatrice de [A'M] est
aussi celle de [C'B']
Car OM = OA'=OC'=OB'
C'M = A'B'
car les 2 segments sont
symétriques par rapport
à la médiatrice [MA']
Or A'B' = ½ AB (Thalès)
C' milieu de AB
Ainsi, C'A = C'B = C'M
M est sur le cercle de
Centre C' et de diamètre [AB]
Ainsi, ABM est rectangle
en M
=> M est le pied de la hauteur
issue de A
Raisonnement identique pour
les deux autres pieds
=> le cercle passant par les
milieux des cotés passe par
le pieds des hauteurs
H : orthocentre
I : intersection
Cercle-hauteur issue de A
IMA' est rectangle en M
=> IA' : diamètre du cercle
B' est sur le cercle de
diamètre IA' =>
angle IB'A' est droit
or (A'B') // (AB) (récip. Thalès)
donc (IB') ⊥ (AB)
(PC) également ⊥ (AB)
=> (PC) // (IB')
Thalès avec :
AB'/AC = ½ et
(PC) // (IB')
=> AI/AH = ½
I est le milieu de AH