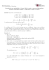Les lois de probabilités

Chapitre 4. Lois de Probabilité
Introduction
•
Il est toujours possible d’associer à une variable
aléatoire une probabilité et définir ainsi une loi de
probabilité. Lorsque le nombre d’épreuves augmente
indéfiniment, les fréquences observées pour le
phénomène étudié tendent vers les probabilités et les
distributions observées vers les distributions de
probabilité ou loi de probabilité.
Identifier la loi de probabilité suivie par une variable
aléatoire donnée est essentiel car cela conditionne le
choix des méthodes employées pour répondre à une
question biologique donnée (chapitre 5 et 6).
Lois discrètes
Loi de Uniforme
En effet
n
∑ i = 1 + 2 + 3 + ... + n
i =1
1 1 + 2 + 3 + ... + n  n(n + 1)
= 
=

2 n + (n − 1) + ... + 1
2
d' où
n
E(X) =
∑i
i =1
n
=
(n + 1)
.
2
Par ailleurs on a
i 2 (n + 1) 2
V ( X ) = E( X ) − E( X ) = ∑ −
4
i =1 n
On doit donc montrer que
n
2
2
i 2 (n + 1) 2 n 2 − 1
−
=
∑
4
12
i =1 n
n
⇔ ∑12i 2 − 3n(n + 1) 2 = n(n 2 − 1)
n
i =1
⇔ ∑12i 2 = n[4n 2 + 6n + 2]
n
i =1
2
n
n 1

⇔ ∑ i 2 = n + + 
i =1
 3 2 6
n
Démonstration par récurrence
La formule
 n2 n 1 
i = n + + 
∑
i =1
 3 2 6
est vraie pour n = 1.
n
2
n
Posons S n : = ∑ i 2 est supposons que
i =1
 n2 n 1 
Sn = n + + 
 3 2 6
on doit avoir
 n2 n 1 
S n +1 = n  + +  + (n + 1) 2
 3 2 6
La formule est vraie pour n + 1 si
 (n + 1)2 (n + 1) 1 
 n2 n 1 
2
n  + +  + (n + 1) − (n + 1)
+
+ =0
2
6
 3 2 6
 3
d' où le résultat!
Loi de Bernoulli
Loi binomiale
Espérance et variance pour la loi binomiale
Stabilité de la loi binomiale
Loi de Poisson
Pour chaque entier k ≥ 1 (fixé) la loi binomiale vérifie la propriété suivante :
P(Sn = k) = C p ( 1 − p)
k
n
k
n−k
λk e− λ
→
,
k!
lorsque n → +∞, sous la contrainte
np = λ
où λ est le nombre moyen de réalisation.
Remarque: Si on reprend l’exemple des rats, on pour n=100 rats on a p=1/4
et λ=25.
Comparaison de la loi binomiale et la loi de Poisson
pour n=100, λ=1, p=0.01
Binomiale
Poisson
Donc en pratique lorsque l’on a un « grand nombre » d’évènements qui suivent une
loi binomiale et qu’on connaît la moyenne λ, on peut utiliser une loi de Poisson.
Démonstration
En effet on a p =
C p (1 − p)
k
n
k
n−k
λ
n
n!
λ 
=
 
k!(n − k )!  n 
λk 
n!  1 
= 
 
k!  (n − k )!  n 
k
 λ
1 − 
 n
n−k
k
 λ
1 − 
 n
n−k



λk 
n
n!  1 
n−k 
(
)
n
= 
−
λ
 

k!  (n − k )!  n 

n
n
Mais d' aprés la formule de Striling (i.e. n! ≈ 2πn   ) on a
e
n!
n
nn
e −k
≈
n−k
(n − k )!
n − k (n − k )
donc
n!  1 
n n−λ
n−k
lim
n − λ ) = lim
(




n → +∞
n → +∞
(n − k )!  n 
n−kn−k 
n
n−λ
= lim 

n → +∞
n−k 
n−k
e −k
n−k
e −k
Pour conclure il reste a montrer que
n−k
n−λ
−k
−λ
=
lim
e
e


n → +∞
n−k 
En effet on a
n−λ


n−k 
n−k
=e
 n−λ 
( n − k ) ln 

 n−k 
=e
 n −λ

( n − k ) ln 
−1+1 
n
−
k


  n − λ 2 
n−λ
 n−λ
ln
− 1 + 1 =
− 1 + O 
− 1 
n−k
 n−k
 n − k  
2

−λ+k
 − λ + k  

=
+ O 
 
n−k
n
−
k
 

Donc
 n −λ

−1+1 
( n − k ) ln 
 n−k

  − λ+k 2 
− λ + k +( n −k )O 
 
  n−k  


e
=e
d' où le résultat.
→ e − λ + k quand n → +∞,
Espérance et variance
Comparaison de la loi binomiale et la loi de Poisson
pour n=500, p=1/365, λ=500/365
Rappel: 1 litre=1000 cm3
Donc ici le nombre moyen de bactéries par boite est 5.
On suppose aussi que le nombre de colonie par boite
est le même que le nombre moyen de bactéries par boites
Stabilité de la loi de Poisson
Loi binomiale négative (des temps d’attente)
Sous les conditions de Bernoulli (épreuves identiques et indépendantes), on
désire connaître la probabilité (d’attendre) de faire X=k épreuves
indépendantes, pour avoir n succès.
Espérance et variance
Loi géométrique ou loi de Pascal
ou binomiale négative avec n=1
Lois continues
Loi Uniforme
Espérance et variance
Loi normale ou loi de Laplace-Gauss
+∞
On admettra que
∫ f ( x)dx = 1 car on ne peut pas calculer cette intégrale par
-∞
des méthodes usuelles.
Espérance et variance
Stabilité de la loi normale
Loi normale centré et réduite
Relation avec la loi normale
Lois déduites de la loi normale
Loi du χ2 de Pearson
Loi de Student
Loi de Fisher-Snedecor
Convergence en loi
Le théorème central limite