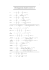Cal I Review

Review of Cal I
Trig Derivatives:
d
[sin u ] 
dx
d
[cos u ] 
dx
d
[tan u ] 
dx
d
[sec u ] 
dx
d
[cot u ] 
dx
d
[csc u ] 
dx
Exponential and Natural Log Functions:
f ( x)  e x
2x
d u
du
[e ]  eu
dx
dx
and
f ( x)  ln(sin( x))
d n
[ x ]  nx n 1
dx
4
3
f ( x)  x  3x  6 x 2  x
Power Rule:
Product Rule:
d
[uv]  uv  vu
dx
f ( x)  x3 cos x
Quotient Rule:
x3  1
f ( x)  2
x 2
d
1 du
u ( x )
or
[ln u ] 
dx
u dx
u
d  u  vu  uv
d  T  BT   TB


OR
2
dx  v 
v
dx  B 
B2
d
u n  nu n1u
dx
Chain Rule:
f ( x)   3 x 2  5 x  1
4
f ( x)  sin 3 (5 x)
f ( x)  tan 5

3x 2  1

Implicit Differentiation:
dy
, given x 3  4 x 2 y 4  3 y 5  9
Find
dx
dy
, given cos( xy )  y 3  4
dx
Find
Integrals:
 f ( x)dx = a set of antiderivatives
 k du  k u  C
 sin(u ) du   cos(u )  C
 cos(u ) du  sin(u )  C
 sec (u ) du  tan(u )  C
2
u
u
 e du  e  C
1
 3
3
  x  3 x  5 dx
x 

Why a set?
Review of Basic Forms
u n 1
n
 u du  n  1  C n  1
 csc(u ) cot(u ) du   csc(u )  C
 sec(u ) tan(u ) du  sec(u )  C
 csc (u ) du   cot(u )  C
2
 1 du  ln u  C

u
 x(5x
2
 4)3 dx
 6x2
dx

3
5
 (4 x  9)
 cos x dx
 3
 sin x

 x sin(6 x )dx
tan x sec2 xdx
 x dx
 2
 x 1
2
x
 2 xe dx
2
Review of Basic Integration Rules
ReviewBasicInverseTrigDerivatives:
d
u
d
u
(arcsin u ) 
(arctan u ) 
dx
dx
1  u2
1  u2
d
u 
(arccos u ) 
dx
1  u2
d
(arcsec u ) 
dx
u
d
(arccsc u ) 
dx
u
u 
d
(arccot u ) 
dx
1  u2
Review Basic Inverse Trig Integration:
du


 2
 a  u2
du



 u u2  a2
 du 
 2
 a  u2
Find the indefinite integral:
1

dx

2
 2  9x

1
dx

2
 x 4x  9



1
25  36 x 2
dx
u
u2 1
u
u2  1
ImproperFractions:
The degree of the numerator is greater than or equal to the degree of the denominator. You must
DIVIDE to change to a "mixed" fraction before you integrate.
 x 1
dx
 2
 x 1
4
 x
dx
 2
 x 1
2
 4x  7
dx

 2x  3
2
1
(Hint: Remember 
 du  ln u  C
u
SeparatingFractions:
x
x x
x
dx   2  dx
 2
1
 x 1
x
4
You CANNOT separate denominators.
 2  8x
dx

2
 1  4x
4