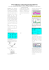Active and Passive Vibration Isolation and Damping via Shunted

Transcription

Université Libre de Bruxelles
F a c u l t é d e s S c i e n c e s A p p l i q u é e s
Active and Passive Vibration Isolation
and Damping via Shunted Transducers
Bruno de Marneffe
quiet side
F
Force Sensor
fc
k
noisy side
quiet side
Electric
circuit
I
I
Controller
Electromagnetic
transducer
fd
Thesis submitted in candidature for the
degree of Doctor in Engineering Sciences
fc
k
V
noisy side
fd
14 December 2007
Active Structures Laboratory
Department of Mechanical Engineering and Robotics
Jury
President : Prof. Alain Delchambre (ULB)
Supervisor : Prof. André Preumont (ULB)
Members :
Prof. Stephen J. Elliott (ISVR - Southampton)
Prof. Johan Gyselinck (ULB)
Dr. Stanislaw Pietrzko (EMPA - Switzerland)
Prof. Paul Sas (KUL - Leuven)
iii
Remerciements
Je voudrais tout d’abord remercier le professeur André Preumont, directeur du
Laboratoire des Structures Actives de l’ULB et promoteur de cette thèse, pour
m’avoir accueilli au sein de son service et m’avoir permis, pendant plus de quatre
ans, de travailler dans des domaines variés et intéressants; ses idées et ses conseils
m’ont été d’une grande aide. Je remercie également tous mes collègues et anciens
collègues pour leur aide, leurs encouragements et l’ambiance chaleureuse qui s’est
instaurée pendant toutes ces années.
Je remercie tout particulièrement Iulian Romanescu et Mihaita Horodinca qui
ont, chacun à leur tour, pris en charge la réalisation des différents dispositifs
expérimentaux. L’aboutissement de ces travaux, et particulièrement de la plateforme de Stewart, doit beaucoup à leurs talents de mécanicien.
Ce travail est la continuation directe de travaux de recherches effectués avant
mon arrivée à l’ULB: je dois beaucoup à mes prédécesseurs qui ont balisé la voie
à suivre. Mes remerciements vont particulièrement à Frédéric Bossens qui m’a, le
premier, appris les rudiments du contrôle de structures. J’exprime également ma
gratitude à Michel Osée, du département BEAMS de l’ULB, et à Jean-Philippe
Verschueren, de Micromega-Dynamics S.A., pour leur patience et leur aide lors de
la mise en oeuvre des différents circuits électroniques. Merci aussi à Arnaud Deraemaeker pour son aide lors de la modélisation de structures piézoélectriques, et à
Mohamed El Ouni, Thomas Lemaı̂tre (stagiaire ESTACA) et Samuel Veillerette
qui ont tous trois participé à la préparation du nouveau vol parabolique. Je tiens
de même à souligner la disponibilité de Gillian Lucy, du département d’anglais
de l’ULB, qui a patiemment relu ce manuscrit: ses commentaires m’ont permis
d’en corriger de nombreuses fautes d’anglais.
Merci enfin à ma famille et à Nadine pour leur soutien et leurs encouragements.
Au cours de ce travail j’ai été supporté par le Pôle d’Attraction Inter-Universitaire
IUAP 5 (Advanced Mechatronics Systems), par l’ESA dans le cadre du programme PRODEX (C90147) et par le Sixième Programme Cadre de l’UE avec
le projet CASSEM (Composite and Adaptative Structures: Simulations, Experimentation and Modelling). J’ai également bénéficié du soutien indirect de projets
de l’UE (InMAR: Intelligent Materials for Active Noise reduction) et de l’ESA
(LSSP: Low Stiffness Stewart Platform et SSPA: Smart Structures For Payloads
And Antennae).
v
Abstract
Many different active control techniques can be used to control the vibrations of
a mechanical structure: they however require at least a sensitive signal amplifier
(for the sensor), a power amplifier (for the actuator) and an analog or digital filter
(for the controller). The use of all these electronic devices may be impractical in
many applications and has motivated the use of the so-called shunt circuits, in
which an electrical circuit is directly connected to a transducer embedded in the
structure. The transducer acts as an energy converter: it transforms mechanical
(vibrational) energy into electrical energy, which is in turn dissipated in the shunt
circuit. No separate sensor is required, and only one, generally simple electronic
circuit is used. The stability of the shunted structure is guaranteed if the electric
circuit is passive, i.e., if it is made of passive components such as resistors and
inductors.
This thesis compares the performances of the shunt circuits with those of classical active control systems. It successively considers the use of piezoelectric
transducers and that of electromagnetic (moving-coil) transducers:
• In a first part, several damping techniques are applied on a benchmark
truss structure equipped with a piezoelectric stack transducer. A unified
formulation is found and experimentally verified for an active control law,
the Integral Force Feedback (IFF), and for various passive shunt circuits
(resistive and resistive-inductive). The use of the so-called “negative capacitance” shunt is also investigated in detail. Two different implementations
are discussed: they are shown to have very different stability limits and
performances.
• In a second part, vibration isolation with electromagnetic (moving-coil)
transducers is introduced. The effects of an inductive-resistive shunt circuit
are studied in detail; an equivalent mechanical representation is found. The
performances are compared with those of resonant shunts and with those of
an active isolation technique. Next, the construction of a six-axis isolator
based on a Stewart Platform is presented: the key parameters and the main
limitations of the system are highlighted.
vii
Contents
Jury
iii
Remerciements
v
Abstract
1 Introduction
1.1 Vibration damping of smart
1.2 Vibration isolation . . . . .
1.3 Outline . . . . . . . . . . .
1.4 References . . . . . . . . . .
vii
structures
. . . . . .
. . . . . .
. . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2 Piezoelectric structures and active trusses
2.1 Some early significant realizations . . . . . . . .
2.2 Piezoelectric material . . . . . . . . . . . . . .
2.2.1 Constitutive equations . . . . . . . . . .
2.2.2 Piezoelectric modes of actuation . . . .
2.2.3 Electromechanical coupling factor . . .
2.3 Uniaxial (d33 ) piezoelectric transducer . . . . .
2.4 Structure with a piezoelectric stack transducer
2.4.1 Governing equations . . . . . . . . . . .
2.4.2 Various eigenvalues problems . . . . . .
2.4.3 Modal coordinates . . . . . . . . . . . .
2.4.4 Placement of the active struts . . . . . .
2.5 Experimental benchmark structure . . . . . . .
2.5.1 Active strut . . . . . . . . . . . . . . . .
2.5.2 Active truss . . . . . . . . . . . . . . . .
2.5.3 Mode shapes and actuator placement .
2.5.4 Model updating . . . . . . . . . . . . . .
2.5.5 Objectives of the work . . . . . . . . . .
2.6 References . . . . . . . . . . . . . . . . . . . . .
ix
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
1
5
7
7
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
11
11
12
12
14
15
16
18
18
19
20
20
21
21
22
22
25
27
27
x
3 Integral Force Feedback
3.1 Introduction . . . . . . . . . . . .
3.2 Open-loop transfer function . . .
3.3 Static displacement . . . . . . . .
3.4 Closed-loop system . . . . . . . .
3.4.1 Global coordinates . . . .
3.4.2 Modal coordinates . . . .
3.4.3 Simplified linear analysis .
3.5 Application to the truss . . . . .
3.5.1 Numerical verifications . .
3.5.2 Root locus . . . . . . . .
3.6 Experimental results . . . . . . .
3.7 Charge (current) control . . . . .
3.8 Softening of the active struts . .
3.9 References . . . . . . . . . . . . .
CONTENTS
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
31
31
31
33
34
34
35
36
37
37
38
39
40
42
44
4 Passive shunt damping
4.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . .
4.1.1 Classical shunts . . . . . . . . . . . . . . . . . . .
4.1.2 Alternative shunts . . . . . . . . . . . . . . . . .
4.2 Electrical admittance of the structure . . . . . . . . . .
4.2.1 Single-mode structure . . . . . . . . . . . . . . .
4.2.2 Multi-mode structure . . . . . . . . . . . . . . .
4.2.3 Generalized electromechanical coupling factor . .
4.3 Damping performances . . . . . . . . . . . . . . . . . . .
4.3.1 Eigenvalue problem . . . . . . . . . . . . . . . .
4.3.2 R shunt . . . . . . . . . . . . . . . . . . . . . . .
4.3.3 Series RL shunt . . . . . . . . . . . . . . . . . .
4.3.4 Parallel RL shunt . . . . . . . . . . . . . . . . .
4.3.5 Sensitivity . . . . . . . . . . . . . . . . . . . . . .
4.3.6 Summary (1): maximum attainable damping . .
4.3.7 Summary (2): optimal values of the components
4.4 Application to the truss . . . . . . . . . . . . . . . . . .
4.5 References . . . . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
45
45
45
47
49
49
50
52
53
54
55
56
58
59
59
60
60
63
5 Active shunt damping with a negative capacitance
5.1 Introduction . . . . . . . . . . . . . . . . . . . . . . .
5.2 Effects on a transducer . . . . . . . . . . . . . . . . .
5.2.1 Parallel negative capacitance . . . . . . . . .
5.2.2 Series negative capacitance . . . . . . . . . .
5.3 Shunt-structure interaction and stability . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
67
67
68
68
70
71
.
.
.
.
.
.
.
.
.
.
CONTENTS
5.4
5.5
xi
5.3.1 Parallel shunt . . . . . . . . . . . . . . . . .
5.3.2 Series shunt . . . . . . . . . . . . . . . . . .
5.3.3 Sensitivity . . . . . . . . . . . . . . . . . . .
5.3.4 Nonlinearity . . . . . . . . . . . . . . . . . .
Experimental results . . . . . . . . . . . . . . . . .
5.4.1 Implementation of the negative capacitance
5.4.2 Impedance measurement . . . . . . . . . . .
5.4.3 R shunts . . . . . . . . . . . . . . . . . . . .
5.4.4 RL shunts . . . . . . . . . . . . . . . . . . .
References . . . . . . . . . . . . . . . . . . . . . . .
6 Single-axis isolation
6.1 Introduction . . . . . . . . . . . . . .
6.2 Classical passive isolators . . . . . .
6.3 Sky-hook damper and IFF . . . . . .
6.4 Passive shunts . . . . . . . . . . . . .
6.4.1 Principles . . . . . . . . . . .
6.4.2 Resistive shunts . . . . . . . .
6.4.3 First-order (RL) shunts . . .
6.4.4 Resonant (RLC) shunts . . .
6.5 Experimental set-up . . . . . . . . .
6.5.1 Isolator . . . . . . . . . . . .
6.5.2 Transducer . . . . . . . . . .
6.5.3 Passive components . . . . .
6.5.4 Experimental results . . . . .
6.6 Active shunts . . . . . . . . . . . . .
6.6.1 Active admittance simulator
6.6.2 Experimental results . . . . .
6.7 References . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
7 Multi-axis isolation
7.1 Introduction . . . . . . . . . . . . . . .
7.2 Active isolator . . . . . . . . . . . . .
7.2.1 Leg design . . . . . . . . . . . .
7.2.2 Closed-loop properties . . . . .
7.2.3 Fröbenius norm . . . . . . . . .
7.2.4 Model of the isolator . . . . . .
7.3 Passive isolator . . . . . . . . . . . . .
7.3.1 Mode shapes of the legs . . . .
7.3.2 Load cell . . . . . . . . . . . .
7.3.3 Flexible joints and membranes
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
71
75
77
78
78
78
79
80
82
82
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
87
87
87
88
91
91
92
93
96
100
100
102
103
104
106
106
107
108
.
.
.
.
.
.
.
.
.
.
111
. 111
. 113
. 113
. 116
. 118
. 119
. 120
. 120
. 122
. 122
xii
CONTENTS
7.4
7.3.4 Transducer . . .
7.3.5 Upper plate . . .
7.3.6 Numerical results
References . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
8 Conclusions
A Electrical representation of a
A.1 Structure at rest . . . . . .
A.2 Modelling of a perturbation
A.3 References . . . . . . . . . .
.
.
.
.
123
124
125
126
131
piezoelectric structure
. . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . .
137
. 138
. 139
. 140
Chapter 1
Introduction
1.1
Vibration damping of smart structures
The importance of the structural damping ratio ξ is highlighted in Fig. 1.1
(Preumont, 2006), which shows, on an example with a single degree-of-freedom
(d.o.f), the influence of ξ on (i) the amplification of the structural response near
the resonance frequency and (ii) the number N of cycles necessary to reduce the
amplitude of the impulse response by 50%. Typical damping values encountered
in various fields of structural engineering are also indicated in the figure. Notice
the very low values for space structures: these are due to the absence of aerodynamic and gravity-induced friction forces as well as the use of stiff, bonded
joints (as opposed to bolted joints) that prevent the dissipation of vibrational energy (Nye et al., 1996). The situation is even worse when the application requires
cryogenic temperatures (such as an InfraRed telescope that needs to be cooled
down), because material damping ratios decrease considerably with temperature;
as an example, aluminium at 40K was found to have a damping ratio as low as
10−4 %, i.e. 2% only of its nominal value at room temperature (Peng et al., 2004).
Smart Materials
Up to some levels, the structural damping ratio can be raised by the use of ViscoElastic Materials (VEMs): see e.g. Nye et al. (1996) for interesting examples of
such passively damped space structures. Another possibility consists in implementing an active control system including sensors, actuators and the appropriate
electronics; structures with such systems are said to be smart or adaptive because
they can adapt to minimize the impact of external perturbations. Many different
kinds of sensors and actuators are commercially available; see e.g. Janocha (1999)
for a good review and explanations. The first part of this thesis considers the
1
2
1 Introduction
N=110
h(t)
Dynamic amplification
dB
Impulse response
50%
0
!
t
dB=54
dB=40
dB=34
dB=20
Mechanical Structures
N=22
N=11
Space Structures
0.001
0.005
Soil Radiation
Civil Engineering
N=1
N=2
0.01
dB=14
0.05
0.1
ø
Figure 1.1: Dynamic amplification at resonance (in dB) and number of cycles
N to reduce the amplitude of the impulse response by 50% as a function of the
damping ratio ξ (the damping scale is logarithmic).
use of piezoelectric materials, which are able to convert an electrical signal into
a deformation (and vice-versa). Active control with piezoelectric elements has
several advantages over passive damping with Visco-Elastic Materials (VEMs):
• The characteristics of VEMs are known to vary rapidly with temperature.
Piezos, by contrast, are suitable in a much larger temperature range. For
example, Bronowicki et al. (1996) found that the transfer function between
piezo actuators and sensors embedded in a truss was nearly constant over
the range ±100◦ C.
• The same applies to the bandwidth: while VEMs are typically efficient only
in a limited frequency range, piezos can be actuated from (almost) DC to
hundreds of kHz.
• Introducing passive damping with VEMs into structures where stresses and
strains are very small, such as in space structures, is a very challenging
problem, while piezoceramics have a virtually unlimited resolution. It requires, of course, appropriate electronics and sensitive enough sensors.
1.1 Vibration damping of smart structures
3
It is often found that active systems, in spite of all the necessary equipment,
introduce less mass than a passive solution made of viscoelastic material. The
main drawbacks of piezos are their nonlinearities (e.g. hysteresis), their limited
stroke (a few micrometers) and the high voltages (up to kilovolts) required for
the actuation. The last two problems are of lesser concern in space, where only
very small actuation forces and strains are needed; Wada (1993) pointed out
that a large strain capability is required only to survive the high dynamic strains
imposed during the launch of the structure into space.
Active trusses and collocated control
y
Active member
4
2
6
8
10
12
14
9
11
13
16
18
20
15
17
19
p1
q
1
3
5
7
f
p2
x
d
Detail of an
active member
Force
transducer
Piezoelectric
linear actuator
Figure 1.2: Schematic representation of an active truss. The active struts consist
of a linear piezoelectric transducer aligned with a force sensor.
The concept of active trusses is quite natural: it consists in replacing one or
several passive bars by active members or active struts (Anderson et al., 1990).
Piezoelectric transducers are ideally suited for this purpose, because of their high
stiffness; other types of transducers based e.g. on electrostrictive materials can
also be used but they are not investigated here. An example of such active strut
is shown in Fig. 1.2, which schematizes a uniaxial piezoelectric actuator (acting
along its main axis) aligned with a force sensor, and its insertion into an active
truss.
An important feature of this active strut is the collocation between the actuator
and the sensor. An actuator/sensor pair is said to be collocated if it is physically
located at the same place and energetically conjugated, such as force and displacement or velocity, or torque and angle (Preumont, 2002). The properties of
collocated systems are remarkable; in particular, the stability of the control loop
4
1 Introduction
is guaranteed when certain simple, specific controllers are used1 . Such controllers
include the so-called “Positive Position Feedback” or PPF (Goh and Caughey,
1985; Fanson and Caughey, 1990), the “Direct Velocity Feedback” or DVF (Balas,
1979) and the “Integral Force Feedback” or IFF (Preumont et al., 1992). Other
controllers such as LQG, H2 or H∞ may be more efficient, but they are also
model-dependent, more complex to implement, and their stability is not guaranteed. Properties of collocated systems are extensively discussed in Preumont
(2002); note that:
1. Only the stability of the closed-loop system is guaranteed (the closed-loop
performances are not).
2. The guaranteed stability only holds as long as ideal equipment is assumed:
in practice imperfections of the actuator/sensor pair or of the electronics
(such as non-linearities or a limited bandwidth) might make the system
unstable, in spite of the collocation.
Note finally that the use of these simple controllers does not exclude the parallel
use of more complex controllers such as LQG; see e.g. Aubrun (1980) or Preumont
(2002, chap. 13) for more information.
Shunt damping
Force
sensor
Piezoelectric
linear transducer
f
Vp
Vf
Charge
amplifier
Voltage
amplifier
a)
Ip
Vc
Vp
Electric
circuit
Controller
b)
Figure 1.3: (a) Active control with a separate sensor/actuator pair; (b) shunt
damping with a piezoelectric transducer.
A typical active control implementation requires at least a sensitive signal amplifier (for the sensor), a power amplifier (for the actuator) and an analog or
digital filter (for the controller), as illustrated in Fig. 1.3a with the active strut
1
it also requires that the control architecture be decentralized, i.e. that the feedback path
include only one actuator/sensor pair, and be thus independent of other sensors or actuators
possibly placed on the structure.
1.2 Vibration isolation
5
described in the previous section. The use of all these electronic devices may be
impractical in many applications and has motivated the use of shunt circuits (Forward, 1979; Hagood and von Flotow, 1991; Hollkamp, 1994), in which no sensor
is used: instead, an electrical circuit is connected to the electrodes of the transducer (Fig. 1.3b). In this configuration, the piezo acts as an energy converter:
it transforms mechanical (vibrational) energy into electrical energy, which is in
turn dissipated in the shunt circuit. No separate sensor is required, and only one
(generally simple) electronic circuit is used.
The stability of the shunted structure is guaranteed if the electric circuit is passive, i.e., if it is made of passive components such as resistors and inductors; when
the circuit is active, as in chapter 5, care must be taken that the shunt does not
destabilize the system.
1.2
Vibration isolation
Quiet side
(e.g. optics or
attitude sensors)
Transmits low frequency
attitude control torque
Attenuates high frequency
disturbances
Noisy side
e.g. attitude actuator (RWA)
(a)
Transmissibility
6 d.o.f.
Isolation
1
n
(b)
Figure 1.4: (a) Principles of a vibration isolation device placed between the “noisy
side” and the “quiet side” of the structure, and (b) isolation objectives.
It is important to distinguish between vibration damping and vibration isolation.
As shown in Fig. 1.1, the damping of a structural mode consists in reducing the
response of the structure near the corresponding natural frequency: the effects
of damping are very narrow-band and hardly noticeable far from the resonance
frequencies. Isolation, on the other hand, consists in reducing the vibration transmission from one part of the structure (sometimes called “noisy side”) to the other
(“quiet side”): the reduction of the transmission generally occurs in a large frequency region. Fig. 1.4a schematizes a situation in which both sides (“noisy”
and “quiet”) are separated by an isolation device. The quiet side contains the
payload, and the noisy side includes the attitude control actuators (Reaction
6
1 Introduction
quiet side
F
Force Sensor
fc
k
a)
Electric
circuit
I
I
Controller
Electromagnetic
transducer
noisy side
fd
quiet side
k
fc
V
noisy side
fd b)
Figure 1.5: Single d.o.f. isolation systems with moving-coil transducers. (a) Active system with force feedback; (b) shunted system.
Wheel Assembly, RWA). The role of the isolator is twofold (Fig. 1.4b): it should
(i) totally isolate the two bodies beyond the cut-off frequency ωn of the attitude
control, and (ii) transmit the positioning commands (torque etc.) below ωn .
The isolator can be passive; in its simplest form it consists of a spring and a
viscous damper positioned in parallel. This system, however, involves a fundamental trade-off, described in chapter 6, which motivated the use of active
systems. Many different kinds of actuators (hydraulic, pneumatic, ...) can be
used to this end, depending on the application, and a wide variety of control laws
have been proposed in the literature. Previous work developed at the ULB (Abu
Hanieh, 2003; Preumont et al., 2007), aiming at space applications, used a force
feedback control law with electromagnetic (moving-coil) transducers, as shown in
Fig. 1.5a.
In this work, a different approach is used, in which there is no feedback loop;
instead, the moving-coil transducer is shunted by an electrical circuit (Fig. 1.5b).
Just as with shunted piezoelectric systems, the transducer directly converts mechanical (vibration) energy into electrical energy, and no sensor is needed. Stability is once again guaranteed if the electrical circuit is passive. Although
shunted voice-coils have been used many times to introduce damping in structures (e.g. Behrens et al., 2005, or Paulitsch et al., 2007), we are not aware of
any isolation system employing shunted voice-coils.
1.3 Outline
1.3
7
Outline
The first part of this thesis deals with the damping of a truss structure equipped
with a piezoelectric stack transducer. It consists of four chapters:
• Chapter 2 introduces the general equations that govern such structures,
and the experimental benchmark structure used in this work. A state-space
model is built and updated so as to fit the experimental measurements.
• Chapter 3 introduces active damping with Integral Force Feedback (IFF);
numerical and experimental results are presented.
• Chapter 4 describes the use of passive electric shunts: resistive and resistiveinductive circuits are considered. An analytical formulation is developed
and numerically validated.
• Chapter 5 investigates the use of an active electric shunt, namely the negative capacitance shunt. Two different implementations are discussed, and
stability is studied with Nyquist plots. Experimental results are presented,
which compare and summarize the performances of the different passive
and active shunts considered in this study.
The second part of this work deals with vibration isolation with shunted electromagnetic (moving-coil) transducers. It consists of two chapters:
• Chapter 6 investigates single-axis isolation. The performances of single-pole
(RL) and resonant (RLC) shunt circuits are analyzed and compared with
those of the Integral Force Feedback; experimental results are presented.
• Chapter 7 extends the results to multi-axis isolation. The construction of a
multi-axis active isolator is presented; it is based on the Stewart Platform
architecture and on a decentralized Integral Force Feedback control law. In
a second step, modifications are introduced on this prototype in such a way
that it can be used with passive shunt circuits.
1.4
References
A. Abu Hanieh. Active Isolation and Damping of Vibrations Via Stewart Platform. PhD thesis, Université Libre de Bruxelles, 2003.
E.H. Anderson, D.M. Moore, and J.L. Fanson. Development of an active truss
element for control of precision structures. Optical Engineering, 29(11):1333–
1341, Nov. 1990.
8
References
J.N. Aubrun. Theory of the control of structures by low-authority controllers. J.
Guidance and Control, 3(5):444–451, Sept.-oct. 1980.
M.J. Balas. Direct velocity feedback control of large space structures. AIAA
Journal of Guidance and Control, 2(3):252–253, 1979.
S. Behrens, A.J. Fleming, and S.O.R. Moheimani. Passive vibration control via
electromagnetic shunt damping. IEEE/ASME transactions on mechatronics,
10(1):118–122, Feb. 2005.
A.J. Bronowicki, L.J. McIntyre, R.S. Betros, and G.R. Dvorsky. Mechanical
validation of smart structures. Smart Materials and Structures, 5:129–139,
1996.
J.L. Fanson and T.K. Caughey. Positive position feedback control for large space
structures. AIAA Journal, 28(4):717–724, April 1990.
R.L. Forward. Electronic damping of vibrations in optical structures. Applied
Optics, 18(5):690–697, March 1979.
C.J. Goh and T.K. Caughey. On the stability problem caused by finite actuator
dynamics in the collocated control of large space structures. International
Journal of Control, 41(3):787–802, 1985.
N.W. Hagood and A. von Flotow. Damping of structural vibrations with piezoelectric materials and passive electrical networks. Journal of Sound and Vibration, 146(2):243–268, 1991.
J.J. Hollkamp. Multimodal passive vibration suppression with piezoelectric materials and resonant shunts. Journal of Intelligent Material Systems and Structures, 5:49–57, Jan. 1994.
H. Janocha. Adaptronics and Smart Structures: Basics, Materials, Design, and
Applications. Springer, 1999. (Editor).
T.W. Nye, A.J. Bronowicki, R.A. Manning, and S.S. Simonian. Applications of
robust damping treatments to advanced spacecraft structures. Advances in the
Astronautical Sciences, 92:531–543, Feb. 1996.
C. Paulitsch, P. Gardonio, and S.J. Elliott. Active vibration damping using an
inertial, electrodynamic actuator. ASME Journal of Vibration and Acoustics,
129:39–47, Feb. 2007.
C.Y. Peng, M. Levine, L. Shido, and R. Leland. Experimental observations
on material damping at cryogenic temperatures. In SPIE 49th International
References
9
Symposium on Optical Science and Technology, Denver, Colorado, August 2-6,
2004., Aug. 2004. http://hdl.handle.net/2014/40006.
A. Preumont. Vibration Control of Active Structures: and Introduction. Kluwer,
2002. 2nd edition.
A. Preumont. Mechatronics: Dynamics of Electromechanical and Piezoelectric
Systems. Springer, 2006.
A. Preumont, J.P. Dufour, and C. Malekian. Active damping by a local force
feedback with piezoelectric actuators. AIAA Journal of Guidance, Control and
Dynamics, 15(2):390–395, March-April 1992.
A. Preumont, M. Horodinca, I. Romanescu, B. de Marneffe, M. Avraam, A. Deraemaeker, F. Bossens, and A. Abu Hanieh. A six-axis single-stage active
vibration isolator based on stewart platform. Journal of Sound and Vibration,
300:644–661, 2007.
B.K. Wada. Summary of precision actuators for space application. Technical
report, Jet Propulsion Laboratory (JPL), 1993. http://citeseer.ist.psu.edu
/344213.html.
10
References
Chapter 2
Piezoelectric structures and
active trusses
This chapter introduces the general equations that govern piezoelectric structures:
it considers successively the constitutive equations of piezoelectric materials, the
different actuation modes, the behavior of uniaxial “d33 ” transducers and how
they are embedded into a general piezoelectric structure. The benchmark truss
structure used in this thesis and its state-space model are also presented.
2.1
Some early significant realizations
Most of the early work on the active damping of structures with piezoelements
was done in the United States and focused on space structures. As early as 1979,
R.L. Forward (Hughes Research Laboratories) demonstrated the feasibility of
the technique: in proof-of-concept experiments, he increased the damping ratio
of a bar in extension and of a membrane mirror prototype. He investigated
passive (inductive) shunting as well as some very simple active control laws with
several non-collocated actuator-sensor pairs (Forward, 1979). One year later he
demonstrated the active damping of a composite mast with a more thorough
theoretical development (Swigert and Forward, 1981; Forward, 1981).
Interest in the field then rose in many research departments, which started investigations on beam and plate structures with PZT patches bonded on them (or
embedded in them): see e.g. the work of Crawley and de Luis (1987), Burke and
Hubbard (1987), Fanson and Caughey (1990) or Hanagaud et al. (1992). They
tried to model analytically this new class of structure as well as the effects that
active control might have on them; collocated controllers such as the Positive
Position Feedback (PPF) were introduced (Goh and Caughey, 1985; Fanson and
11
12
Caughey, 1990).
However, all these experiments concerned ‘d31 ’ piezoactuators, i.e. thin patches
of piezoceramic (see Fig. 2.1b), and plate structures. Research on active trusses,
by contrast, began in the late 80’s: see e.g. the work of Anderson et al. (1990),
Fanson et al. (1989), Chen et al. (1989) or Bronowicki et al. (1996) who developed active members made of piezo transducers and verified their compatibility
with space applications: temperature dependance, linearity, power consumption,
bandwidth, etc.
It was found during this period that collocated force or velocity feedback on
the active strut can be used to tailor the strut mechanical impedance and thus
maximize the energy dissipated in the active strut; the usefulness of force feedback
to this end was stressed (Chen et al., 1989). Integral Force Feedback (IFF), in
which the collocated force in the strut is integrated, was investigated at the
ULB from 1988 on; experimental results underlined its efficiency as well as its
guaranteed stability (Preumont et al., 1992).
In a second step, proof-of-concept set-ups were actually tested in space: see e.g.
the ACTEX experiment (Nye et al., 1999), which implemented several active
control laws on a secondary payload riding on a spacecraft, the CFIE experiment
(Loix et al., 1997), which actively damped a piezoelectric plate embarked in
the space shuttle, or the CASTOR experiment (Bousquet et al., 1997), which
introduced various damping technologies on a truss mock-up on board the MIR
space station. In spite of these experimental demonstrations, however, we are not
aware of any actual space structure implementing active control with piezoelectric
transducers.
2.2
2.2.1
Piezoelectric material
Constitutive equations
The piezoelectric constitutive equations were standardized in 1988 by the IEEE
association (IEEE Std., 1988). Assuming linear characteristics and constant temperature, they can be written in tensorial form:
Tij = cE
ijkl Skl − ekij Ek
(2.1)
Di = eikl Skl + εSik Ek
(2.2)
where the usual summation convention on repeated indices has been used and
i, j, k, l take a value from 1 to 3. Tij and Skl are the stress and strain tensors, respectively, while Di and Ek represent the electrical displacement and
electric field vectors. cE
ijkl are the elastic constants under constant electric field
2
(Hooke’s tensor, N/m ), εSik the dielectric constants under constant strain (in
Coulomb/(V olt.m) or F arad/m) and ekij (in Coulomb/m2 or N ewton/(V olt.m))
2.2 Piezoelectric material
13
are the material constants that effectively couple the mechanical and electrical
properties of the material.
Thanks to the many symmetries of the mechanical tensors, an easier matrix
notation can be used instead of the tensorial one. Introducing the stress and
strain vectors 1 as:
 


T11 
S11 








T22 



S22 








 


T33
S33
T =
(2.3)
and
S=
T23 
2S23 






 








T 
2S 


 31 

 31 

T12
2S12
respectively, Eq. 2.1 and 2.2 can be rewritten in the more compact matrix form:
T = [cE ]S − [e]t E
(2.4)
S
D = [e]S + [ε ]E
(2.5)
where [cE ], [e] and [εS ] are (6 × 6), (3 × 6) and (3 × 3) matrices, respectively,
and [.]t represents the matrix transposed. In this notation, S and E have been
chosen as the two (vectorial) independent variables, and (T , D) as the dependent
variables. This choice is not unique: for example, T and E are often chosen as
the dependent variables instead. Eq. 2.4 and 2.5 become in this case:
S = [sE ]T + [d]t E
(2.6)
T
D = [d] T + [ε ]E
(2.7)
where [sE ] = [cE ]−1 is the compliance matrix under constant electric field, [d] is
another (3 × 6) coupling matrix in Coulomb/N ewton or m/V olt and the superscript [.T ] has been added on ε to emphasize the fact that it has been measured
under constant stress: it is thus different from εS . The importance of the electrical and mechanical boundary conditions on the material properties is underlined
in the following. Some useful relations between the matrices are:
[e] = [d][cE ]
(2.8)
cD = cE + et {εS }−1 e
D
E
t
T −1
s = s − d {ε }
εS = εT − d[cE ]dt
d
(2.9)
(2.10)
(2.11)
where the [.D ] superscript means constant-charge (Q = 0) boundary conditions.
See e.g. the IEEE standards (1988) for a complete list of all the possible relations.
1
notice the doubling of the non-diagonal terms of Skl : the last three components of S represent shear angles.
14
2.2.2
Piezoelectric modes of actuation
Thanks to many crystal symmetries, the material coupling matrices [d] and [e]
have few non-zero components (Cady, 1946). Eq. 2.6 and 2.7 can be developed
explicitly; for PZT (Lead Zirconate Titanate) ceramics or PVDF (Polyvinylidene
Difluoride) polymer, they are:
Actuation:

 

  
S11 
s11 s12 s13 0
0
0 
T11 
0
0 d31








 


s12 s22 s23 0
T22 
0
0 d32 
S22 
0
0
 


 E1 





 
 
 




S33
0 d33 
s13 s23 s33 0
0
0  T33
 0
=
0
 T23  +  0 d24 0  E2 
2S
0
0
s
0
0


23
44
 E3

 

 
 

2S31 
 0
d15 0




T31 
0 
0
0
0 s55 0  




 


T12
2S12
0
0
0
0
0
0
0
0 s66
{z
}
|
{z
}
|
compliance
coupling
(2.12)
Sensing:
 


T11 


  
 

T22 
  T


ε1 0 0 E1 
D
0
0
0
0
d
0

 
 1
15
T33
D2 =  0
0
0 d24 0 0
+  0 εT2 0  E2 (2.13)
T23 

 
 


0 0 εT3
D3
E3
d31 d32 d33 0
0 0 




T
|
{z
}
{z
}
|
31


 
T12
permittivity
coupling
where, by convention, the coordinate direction 3 coincides with the polarization
direction of the ceramic. PZT materials are isotropic in the plane, and thus have
d31 = d32 and d24 = d15 . By contrast, the d31 and d32 coefficients of PVDF
can be made different, which allows a certain amount of decoupling between the
directions 1 and 2; PVDF materials also have d24 = d15 = 0.
According to Eq. 2.12, when an electric field E3 is applied parallel to the polarization direction of a PZT material, the piezo transducer expands along its
thickness (d33 ) and shrinks in the in-plane directions, because the d31 and d32
coefficients are negative. By contrast, if an electric field E1 or E2 is applied
perpendicularly to the polarization direction, a shear deformation (d15 or d24 )
appears in the transducer. On a macroscopic scale, three different transduction
modes are possible, all illustrated in Fig. 2.1:
• In the thickness or d33 mode, several thin slices of PZT are stacked together
and separated by electrodes; the direction of expansion is parallel to the
electric field.
• In the in-plane or d31 mode, a thin piezoelectric film is bonded on (or embedded in) a plate structure and creates a bending moment. The direction
2.2 Piezoelectric material
15
ÉL = nd 33V
P
P
+
a) d33
V
_
L
E P t
V
b) d31
ÉL
ÉL = Ed 31L
Supporting structure
ÉL
í = d15 E1
1
c) d15
í
E = V=t
E1
P
3
L0
V
ÉL = íL0
Figure 2.1: The three actuation modes (d33 , d31 and d15 ) of PZT piezoelectric
transducers. P indicates the direction of polarization.
of expansion is perpendicular to the electric field.
• In the shear or d15 mode, the electric field is applied perpendicular to the
polarization direction. The transmission from shear actuation of the piezo
to the structure (or vice-versa) requires a specific mechanical design; see
e.g. Benjeddou et al. (1997) for more details.
This thesis deals exclusively with d33 transducers which, thanks to their shape
and stiffness, can easily be embedded into truss-like structures.
2.2.3
Electromechanical coupling factor
Piezoelectric electromechanical coupling factors are material constants that measure the effectiveness of the conversion of mechanical energy into electrical energy
(and vice-versa); they play a vital role in shunt damping of piezoelectric structures as described in chapters 4 and 5. Three different factors (one per actuation
mode) are defined by:
q
T
• thickness mode: k33 = d33 / sE
33 ε3
q
T
• in-plane mode: k31 = k32 = d31 / sE
11 ε3
16
q
T
• shear mode: k15 = k24 = d15 / sE
55 ε1
or, more synthetically, if the mechanical force is measured in the j th direction
and the electrical field in the ith direction:
q
kij = dij / sjj εTi
(2.14)
(Hagood and von Flotow, 1991). PZT ceramics typically have k33 ≈ k15 ≈ 0.7
and k31 ≈ 0.3. The electromechanical coupling factor can be interpreted as the
ratio between the amount of energy that is converted during a quasi-static loading
cycle and the maximal energy stored in the transducer during the same cycle; see
e.g. Preumont (2006, p. 103) for a demonstration. Electromechanical coupling
factors are most easily measured by means of an impedance measurement as
described in chapter 4.
Because this work is devoted to structures with uniaxial d33 transducers, the
short notation ‘k’ is used hereafter to denote the longitudinal coupling factor k33 .
2.3
Uniaxial (d33 ) piezoelectric transducer
Electrode
+
Cross section: A
Thickness: t
# of disks in the stack: n
l = nt
_
Electric charge:
Q = nAD
Capacitance:
C = n2"A=l
Free piezoelectric expansion:
î = d 33nV
ã
Charge driven: î = nd33Q
C
Voltage driven:
Figure 2.2: Piezoelectric linear transducer.
Consider the piezoelectric linear transducer of Fig. 2.2: in accordance to §2.2.2,
it is made of n identical slices of piezoceramic material stacked together, each of
them polarized through the thickness. If one assumes that the stress, the strain,
the electric field and the electric displacement are one-dimensional and parallel
to the direction of polarization, the constitutive equations (2.12) and (2.13) for
2.3 Uniaxial (d33 ) piezoelectric transducer
the piezoelectric material reduce to:
½ ¾ · T
¸½ ¾
D
ε
d33 E
=
S
d33 sE
T
17
(2.15)
where the subscripts [.]3 or [.]33 are implicitly assumed (D instead of D3 etc).
If all the electrical and mechanical quantities are uniformly distributed in the
transducer, the global constitutive equations are obtained by integrating Eq. 2.15
over the volume of the transducer; using the notations of Figure 2.2, one finds:
½ ¾ ·
¸½ ¾
Q
C
nd33
V
=
(2.16)
∆
nd33 1/Ka
f
where Q = nAD is the total electric charge on the electrodes of the transducer,
∆ = Sl is the total extension (l = nt is the length of the transducer), f = AT
is the total force and V is the voltage applied between the electrodes, resulting
in an electric field E = V /t = nV /l. The capacitance of the transducer with
no external load (f = 0) is C = εT An2 /l, and Ka = A/sE l is the stiffness with
short-circuited electrodes (V = 0). Note that the electromechanical coupling
factor k (§2.2.3) can be defined alternatively by
k2 =
d33 2
n2 d33 2 Ka
=
sE εT
C
Alternative forms of Eq. 2.16 are e.g.:
½ ¾ ·
¸½ ¾
Q
C(1 − k 2 ) nd33 Ka
V
=
f
−nd33 Ka
Ka
∆
or
½ ¾
·
¸½ ¾
Ka
V
1/Ka −nd33
Q
=
f
C
∆
C(1 − k 2 ) −nd33
(2.17)
(2.18)
(2.19)
from which two important relations can be deduced:
1. The capacitance of the transducer under constant-strain (denoted C S ) is:
¯
Q ¯¯
S
= C(1 − k 2 )
(2.20)
C = ¯
V ∆=0
2. The stiffness of the transducer with open electrodes (Q = 0) is
¯
Ka
∆ ¯¯
=
f ¯Q=0 (1 − k 2 )
(2.21)
18
Because k 2 ≈ 0.5 for PZT, the stiffness as well as the capacitance depend significantly on the boundary conditions, which has important consequences for the
different shunt mechanisms (chapters 4 and 5). Note that C S is more a convenient mathematical coefficient than a ‘real’ physical parameter. Indeed, it cannot
be measured directly: it is impossible to produce a perfect clamping that would
guarantee a real constant-volume measurement, and other methods imply highfrequency measurements (see Eq. 4.8) which are not practical either. The IEEE
standards (1988) recommend instead separate measurements of C and k, and
then the use of Eq. 2.20 to obtain C S .
2.4
2.4.1
Structure with a piezoelectric stack transducer
Governing equations
Consider the linear structure of Fig. 2.3, assumed undamped for simplicity, and
equipped with a discrete, massless piezoelectric stack transducer as discussed
in the previous section. A voltage V is applied across the electrodes of the
transducer, and an electric charge Q flows onto them; there is a relation between
Q and V that will be discussed in chapter 4.
Structure
Q
Piezoelectric
Transducer
Figure 2.3: General linear structure equipped with a piezoelectric stack transducer.
The dynamic equations of the structure (without the piezo) are, in Laplace variables:
¡
¢
M s2 + K x = F
(2.22)
where K and M are the stiffness and mass matrices of the structure, obtained
2.4 Structure with a piezoelectric stack transducer
19
e.g. by means of a Finite Element model, and F is the vector of external forces.
Here we consider that the only forces exerted on the structure come from the
transducer:
F = bf
(2.23)
where b is the projection vector relating the end displacements of the strut to
the global coordinate system, and f is the force exerted by the piezo (Eq. 2.18
or 2.19). Similarly, the elongation ∆ of the transducer is linked to the structural
displacement by:
∆ = bT x
(2.24)
The coupled equations governing the piezoelectric structure can be found by
combining Eq. 2.22 to Eq. 2.24 with Eq. 2.18; they are
¡
¢
M s2 + K + Ka bbT x = bKa nd33 V
(2.25)
C(1 − k 2 )V + nd33 Ka bT x = Q
(2.26)
Note that the mass of the actuator can easily be added to the mass matrix M if
necessary.
2.4.2
Various eigenvalues problems
Analyzing further Eq. 2.25 and 2.26, three different eigenvalue problems can be
defined, corresponding respectively to the boundary conditions f = 0, V = 0 and
Q = 0.
1. From Eq. 2.25, the eigenvalue problem when the axial stiffness of the actuator is cancelled, i.e. Ka = 0, is given by:
¡
¢
M s2 + K x = 0
(2.27)
2. If V = 0, i.e. if the piezo is short-circuited, the structure obeys:
¡
¢
M s2 + K + Ka bbT x = 0
(2.28)
3. Finally, if the structure is charge-driven instead of voltage-driven, V can be
eliminated from Eq. 2.25 and 2.26; the new equation is:
µ
¶
Ka
Ka
Q
2
T
Ms x + K +
bb
x=b
nd33
(2.29)
2
2
1−k
1−k
C
and if the structure is open-circuited, i.e. if Q = 0, it obeys:
µ
¶
Ka
2
T
Ms + K +
bb
x=0
1 − k2
(2.30)
which is the same as Eq. 2.28 but with the short-circuit stiffness Ka replaced
by the open-circuit one Ka /(1 − k 2 ).
20
The solutions of these eigenvalue problems are three different sets of natural
frequencies; in this work the natural frequencies when Ka = 0 are called zi
(i = 1, . . . , n), those when the piezo is short-circuited are called ωi and those
when the piezo is open-circuited are called Ωi .
2.4.3
Modal coordinates
The characteristic equations (2.25) and (2.26) can be transformed into modal
coordinates according to x = Φα, where Φ = (φ1 , . . . , φn ) is the matrix of the
mode shapes, solutions of the eigenvalue problem (2.28). The mode shapes are
normalized according to
ΦT M Φ = diag(µi )
(2.31)
and
ΦT (K + Ka bbT )Φ = diag(µi ωi2 )
(2.32)
with ωi the ith natural frequency of the structure with short-circuited electrodes
and µi the ith modal mass. The important parameter
νi =
φTi (Ka bbT )φi
(φTi b)2 Ka
=
µi ωi2
φTi (K + Ka bbT )φi
(2.33)
can then be defined; it represents the ratio between (twice) the strain energy
in the actuator and (twice) the total strain energy when the structure vibrates
according to mode i: it is the fraction of modal strain energy (Preumont et al.,
1992). Physically, νi can be interpreted as a compound indicator of controllability
and observability of mode i by the transducer. It is readily available in most Finite
Element Analysis softwares.
2.4.4
Placement of the active struts
Parallel to the development of adaptive or intelligent transducers, research has
been conducted on the optimal placement of the active struts. Indeed, the structures are generally so large that it would be computationally too intensive to test
all the different possibilities. A wide variety of optimisation algorithms were proposed to this end in the literature; two popular examples are the Simulated Annealing method (Chen et al., 1991) and the Genetic Algorithm method (e.g. Rao
et al., 1991). See also Padula and Kincaid (1999) for a review of the different
placement strategies.
Although these methods are effective, they fail to give a clear physical justification
for the choice of the struts placement. An alternative, more physical method has
been used (with some variations) e.g. by Fanson et al. (1989), Preumont et al.
2.5 Experimental benchmark structure
21
(1992) or Bronowicki et al. (1999): it merely consists in placing the transducer in
the struts with maximal fraction of modal strain energy νi , where i is the mode
to be controlled. This method was chosen when designing the benchmark truss
structure of this study. Lu, Utku, and Wada (1992) have considered another
strategy, based on a pole placement technique; their method turned out to select
the struts with the highest νi as well.
2.5
2.5.1
Experimental benchmark structure
Active strut
Piezo
transducer
(PI P010.30H)
Prestressing
wire
a)
b)
Figure 2.4: a) The piezoelectric stack actuator built for this work; b) (not to
scale) another commercially available design (PI 840-30) and its collocated force
sensor.
A piezoelectric stack transducer was specially built for this work; it is represented
in Fig. 2.4a. It is made of a hollow cylindrical stack actuator (PI P-010.30H);
an internal Kevlar wire (φ = 1.1mm) exerts a 16 kg prestress. The prestress
is necessary because such stack transducers cannot withstand traction forces.
Other commercially available transducers, such as that in Fig. 2.4b, introduce the
prestress via an external envelope instead: it is stronger, but also stiffer, which
tends to reduce the effective electromechanical coupling factor k as demonstrated
in Preumont (2006, p. 110).
The main characteristics of the transducer, obtained from measurements, are
22
presented in Table 2.1. Ka could not be measured directly but was identified
from model updating as explained below. The effective coupling factor k 2 of the
transducer is a little higher with the prestress than without (0.36 vs. 0.325);
the reasons for this behavior are unclear (it may be due to nonlinearities of the
ceramic).
Material type
Dimensions (mm)
Ka
C
k2
n (number of discs)
PIC-151
L = 40, Ri = 2.5, Re = 5
≈ 90N/µm
122nF
0.36
60
Table 2.1: Identified stack actuator characteristics.
2.5.2
Active truss
The truss structure used in this work is depicted in Fig 2.5. It consists of 12 bays
of 140 mm each, made of steel bars of 4 mm diameter connected with plastic
joints; it is clamped at the bottom. It is equipped with two active struts (piezo
transducer + collocated force sensor B&K 8200) as indicated in the figure. This
truss was already considered in the experimental setup of Preumont et al. (1992),
but in this work one of the piezoelectric transducers has been replaced by the
new one presented in §2.5.1. The second transducer is an out-dated high-voltage
Philips PXE-HPA1 piezo stack with a very low k factor; in this work it is used
only as an excitation source.
2.5.3
Mode shapes and actuator placement
A Finite Element (FE) model of the truss has been constructed with the commercial software SAMCEF. The passive struts are modelled with beam elements,
and the active ones are obtained by Guyan’s reduction of a separate model with
piezoelectric volume elements (Fig. 2.6). The reduction is performed directly
in SAMCEF; this procedure was necessary because SAMCEF’s libraries do not
include any piezoelectric beam element. After reduction, the transducer model
has only 12 mechanical variables (6 d.o.f. at its end points) and 1 electrical variable (voltage): it behaves like a beam element with uniaxial (d33 ) piezoelectric
transduction capabilities.
The first two mode shapes of the passive truss (i.e., when all the struts are
identical - no piezo yet) are shown in Fig. 2.7; the arrows indicate the approximate
direction of deformation. The fractions of modal strain energy νi are shown in
23
Force
sensor
b)
Piezoelectric
transducer
Strut 1
Strut 1:
damping +
Measurements
Strut 2
Strut 2:
Excitation
a)
c)
Figure 2.5: a) truss structure used in the experiment; b) detail of an active strut;
c) disposition of the active struts (zoom).
12 mechanical d.o.f.
1 electrical d.o.f.
Figure 2.6: Full FE model of the stack with piezoelectric volume elements and
condensed structure with 12 mechanical d.o.f. (6 at each endpoint) and 1 electrical d.o.f.
24
Mode 2
(21.7 Hz)
Mode 1
(17.8 Hz)
strut 2
strut 2
strut 1
strut 1
Maximum strain
energy in strut 1
Maximum strain
energy in strut 2
z
x
y
Figure 2.7: Structural mode shapes when all the struts are passive and identical. Top view is also shown; the arrows indicate the (approximate) direction of
deformation.
Table 2.2 for the first six modes and the two struts. From the figure and the table
one can see that strut 1 has a large influence on mode 1 and almost no influence
on mode 2, and that the opposite occurs for strut 2. This result motivated the
positions of the transducers in the actual truss.
ωi /2π
mode
1
2
3
4
5
6
17.78
21.68
79.75
80.97
103.69
168.94
νi (%)
strut 1 strut 2
13.67
3.29
0.078
11.20
3.18
2.04
0.025
3.05
0.091
2.55
0.072
2.81
Table 2.2: Computed natural frequencies (in Hz ) and fractions of modal strain
energies for strut 1 and 2 when all the struts are passive and identical.
2.5.4
25
Model updating
I1(Q1)
V2
V1
State-Space
Model
F1
Figure 2.8: Matlab state-space model of the truss. Inputs are the current (or
charge) flowing into strut 1 (I1 or Q1 ) and the voltage imposed at strut 2 (V2 ),
while the outputs are the voltage and the force in strut 1 (V1 , F1 ).
The SAMCEF FE model has been exported into a more flexible MATLAB statespace model represented in Fig. 2.8; this required the development of a special
procedure based on a Craig-Bampton reduction of the FE model (de Marneffe
and Deraemaeker, 2006). The inputs consist of I1 , the current in strut 1, and of
V2 , the voltage in strut 2; the outputs consist of V1 and F1 , the voltage and the
force in strut 1. Alternatively, it is possible to use V1 as input and I1 as output
instead.
Three open-loop Frequency Response Functions (FRF) were computed with this
model: F1 /V2 , V1 /I1 and F1 /V1 . The FE model was thoroughly updated to obtain
the best fit between these curves and the experimental ones; the parameters
involved in the model updating are the truss’s Young modulus E, the inertia of
the lumped mass placed at the top, and the transducers’ material constants c33 ,
d33 and εS3 (whose impact on the macroscopic coefficients Ka , C and k 2 of the
strut is explained in §2.3). This updating process was a delicate task because it
involved the fitting of three different curves. The priority was always given to the
fit of the impedance V1 /I1 , because the performances and stability of the shunt
circuit are extremely sensitive to it (chapters 4 and 5). Note that, because the
actual transducer is stiffer than expected, the results presented in this work differ
slightly from the numerical ones presented in Preumont et al. (2007), which were
obtained before the model updating.
The final results are shown in Fig. 2.9: the matching is very good up to about
50 Hz, which is sufficient for our purpose (no attempt was made to fit the modes
around 100 Hz). The first curve (F1 /V2 , Fig. 2.9a) is used throughout this work
to illustrate the effectiveness of the different damping methodology; both modes
have approximatively the same amplitude in the FRF, thanks to the respective
actuator and sensor positions. The second curve (V1 /I1 , Fig. 2.9b) is the electrical
impedance of the strut when it is installed in the truss; its poles are at ±jΩi and
26
þ ( î)
F1
V2
0
-90
V1
I1
45
0
-45
-90
-180
Ò1
110
dB
Ò2
100
Numerical
!2
90
Experimental
20
15
25
30
!1
80
35
16
18
22
b)
a)
dB
Hz
20
F1
V1
!1
Experimental
!2
z2
Experimental
Numerical
Numerical
z1
1
Hz
10
c)
100
Figure 2.9: Comparison between numerical and experimental results: a) FRF
between the voltage at strut 2 and the force in strut 1; b) electrical impedance
V /I of strut 1; c) open-loop FRF between the voltage and the force in strut 1.
2.6 References
27
its zeros at ±jωi as demonstrated in chapter 4. The third curve (F1 /V1 ) is the
open-loop FRF of the strut: its zeros are at ±jzi and its poles at ±jωi .
Finally, Table 2.3 presents some important structural parameters of the active
truss (i.e. when the active struts have been embedded in the truss), when strut 1
is used for control. Notice the large change in νi from Table 2.2 to Table 2.3, due
to the stiffness of the piezo which is larger than that of the passive struts. The
Ωi are quite close to the ωi , indicating that the electrical boundary conditions
(short-circuit vs. open circuit) have a weak influence on the structure: this has
an important impact on the shunt damping performances (chapters 4 and 5).
On the other hand, z1 is really low compared to ω1 : the importance of this will
appear in the next chapter (active damping with Integral Force Feedback).
ωi (Hz)
νi (%)
ξi (%)
Ωi (Hz)
zi (Hz)
mode 1
18.91
3.0
0.18
19.02
2.02
mode 2
22.52
0.16
0.18
22.53
22.35
Table 2.3: Identified structural characteristics of the active truss when strut 1 is
used for control.
2.5.5
Objectives of the work
This thesis is concerned with the implementation of shunt circuits and how they
compare with active solutions such as IFF. To this end, we concentrate on the
damping of mode 1 only, meaning that all the damping techniques are implemented with strut 1. This is why only strut 1 was replaced with a new, more
effective transducer: strut 2 is used only as an excitation source and did not need
to be upgraded.
As demonstrated numerically in Preumont et al. (2007), all the results can be
transposed to mode 2 simply by implementing the control scheme on strut 2
instead of 1. Both modes can also be damped simultaneously, by implementing
two independent control loops, but this is not the objective of this work.
2.6
References
1341, Nov. 1990.
28
References
A. Benjeddou, M.A. Trindade, and R. Ohayon. A unified beam finite element
model for extension and shear piezoelectric actuation mechanisms. Journal of
Intelligent Material Systems and Structures, 8:1012–1025, Dec. 1997.
P. W. Bousquet, P. Guay, and F. Mercier. CASTOR active damping experiment, preliminary flight results. Journal of Intelligent Material Systems and
Structures, 8(9):792–800, 1997.
1996.
A.J. Bronowicki, N.S. Abhyankar, and S.F. Griffin. Active vibration control
of large optical space structures. Smart Materials and Structures, 8:740–752,
1999.
S.E. Burke and J.E. Hubbard. Active vibration control of a simply supported
beam using a spatially distributed actuator. IEEE control system magazine,
pages 25–30, Aug. 1987.
W. G. Cady. Piezoelectricity: An Introduction to the Theory and Applications of
Electromechanical Phenomena in Crystals. Mc Graw-Hill, New-York, London,
1946.
G.S. Chen, B.J. Lurie, and B.K. Wada. Experimental studies of adaptive structures for precision performance. In SDM Conference, pages 1462–1472. AIAA
paper 89-1327 CP, 1989.
G.S. Chen, R.J. Bruno, and M. Salama. Optimal placement of active/passive
members in truss structures using simulated annealing. AIAA Journal, 29(8):
1327–1334, Aug. 1991.
E.F. Crawley and J. de Luis. Use of piezoelectric actuators as elements of intelligent structures. AIAA Journal, 25(10):1373–1385, Oct. 1987.
B. de Marneffe and A. Deraemaeker. State-space models of structures equipped
with MFCs (macro-fibres composites) in Matlab/Simulink. InMAR technical
report D173 (WA2.1), ULB, 2006.
J.L. Fanson, G.H. Blackwood, and C.C. Chu. Active-member control of precision
structures. In SDM Conference, pages 1480–1494. AIAA paper 89-1329 CP,
1989.
References
29
Optics, 18(5):690–697, March 1979.
R.L. Forward. Electronic damping of orthogonal bending modes in a cylindrical
mast - experimental. J. Spacecraft, 18(1):11–17, Jan.-Feb. 1981.
S. Hanagaud, M.W. Obal, and A.J. Calise. Optimal vibration control by the
use of piezoceramic sensors and actuators. Journal of Guidance, Control and
Dynamics, 15(5):1199–1206, Sept.-Oct. 1992.
IEEE Std. IEEE standard on piezoelectricity, 1988. ANSI/IEEE Std 176-1987.
N Loix, A. Conde Reis, P. Brazzale, J. Detteman, and A. Preumont. CFIE:
In-orbit active damping experiment using strain actuators. In Space Microdynamics and Accurate Control Symposium, Toulouse, France, May 1997.
L.Y. Lu, S. Utku, and B.K. Wada. On the placement of active members in
adaptive truss structures for vibration control. Smart Materials and Structures,
1:8–23, 1992.
T.W. Nye, R.A. Manning, and K. Qassim. Performance of active vibration control
technology: The ACTEX flight experiments. Smart Materials and Structures,
8:767–780, 1999.
S.L. Padula and R.K Kincaid. Optimization strategies for sensor and actuator
placement. Technical report TM-1999-209126, NASA Langley Research Center,
1999.
A. Preumont, B. de Marneffe, A. Deraemaeker, and F. Bossens. The damping of
a truss structure with a piezoelectric transducer. Computers and Structures,
March 2007. in press, corrected proof.
30
References
S.S. Rao, T.S. Pan, and V.B. Venkayya. Optimal placement of actuators in
actively controlled structures using genetic algorithms. AIAA Journal, 29(6):
942–943, June 1991.
C.J. Swigert and R.L. Forward. Electronic damping of orthogonal bending modes
in a cylindrical mast - theory. J. Spacecraft, 18(1):5–10, Jan.-Feb. 1981.
Chapter 3
Integral Force Feedback
3.1
Introduction
Active damping of structures with Integral Force Feedback (IFF) was introduced at the beginning of the 90’s (Preumont, Dufour, and Malekian, 1992) and
has since been thoroughly studied both theoretically and experimentally (e.g.
Bossens, 2001 or Preumont, 2002). In this chapter we summarize the main theoretical results, and we apply experimentally the technique to the truss structure:
these experimental results will serve as a reference for comparison when we introduce passive and active shunt damping (chapters 4 and 5). We also study
in more detail the analytical prediction of the performances, which caused some
difficulties in the early phase of the work. Finally, the problematic of the truss
softening is briefly considered.
3.2
Open-loop transfer function
We assume that a force sensor is collocated with the piezoelectric transducer
as described in Fig. 2.5: it measures the axial force f acting along the strut.
According to Eq. 2.18, this force is given by:
f = Ka (∆ − δ)
(3.1)
where δ , nd33 V is the unconstrained piezoelectric expansion and ∆ = bT x is
the axial elongation of the transducer. δ is often used in the so-called “thermal
analogy” in which, as for thermal loads, the piezoelectric effects are modelled as
equivalent loads acting on the passive structure. The response of the structure to
a voltage input was given in §2.4.1; it can be written, if s is the Laplace variable:
¡
¢
M s2 + K + Ka bbT x = bKa δ
(3.2)
31
32
which gives:
¡
¢−1
x = M s2 + K + Ka bbT
bKa δ
(3.3)
¡
¢
−1
M s2 + K + Ka bbT
is called the dynamic flexibility matrix as it relates the
structural displacements to the forces that are exerted on it1 . If one goes into
modal coordinates according to
x=
n
X
αi φi
(3.4)
i=1
with φi (i = 1, . . . , n) the mode shapes defined in §2.4.3 (short-circuited electrodes) and αi the modal amplitudes, Eq. 3.2 becomes:
n
X
s2 αi M φi +
i=1
n
X
¡
¢
αi K + Ka bbT φi = bKa δ
(3.5)
i=1
which gives, after left multiplication by φTi and the use of the orthogonality
relations (2.31) and (2.32):
x=
n
X
i=1
and thus:
φ φT
¡ i i 2 ¢ bKa δ
µi s2 + ωi
n
X
(bT φi )2 Ka
∆=b x=
δ
µ (s2 + ωi2 )
i=1 i
T
(3.6)
(3.7)
Introducing Eq. 3.7 into Eq. 3.1, one finds the open-loop transfer function of the
active strut:
Ã n
!
X (bT φi )2 Ka ω 2
f
i
− 1 Ka
(3.8)
G(s) = =
2
2 + ω2
δ
µ
ω
s
i
i
i
i=1
!
Ã n
X νi ω 2
i
− 1 Ka
(3.9)
=
2 + ω2
s
i
i=1
where Eq. 2.33 defining the fraction of modal strain energy νi has been used.
The corresponding FRF is represented in Fig. 3.1 for a fictitious, undamped,
three-mode structure; it has alternating poles and zeros because of its collocated
nature (Preumont, 2002). From Eq. 3.9 the poles are at the short-circuit natural
frequencies ±jωi , and it is shown in §3.4 that the zeros are at the natural frequencies ±jzi (those with Ka = 0). Eq. 3.9 was developed for an undamped structure;
1
For structures with n d.o.f. and a single transducer, b and x are (n × 1) vectors, K and M
are (n × n) matrices and V is a scalar.
3.3 Static displacement
33
G(!)
Ka
0
Figure 3.1: Open-loop FRF G(ω) = f /δ of an active strut embedded into a
fictitious, undamped, three-mode mechanical structure.
structural damping can be easily taken into account by adding a damping term
in the denominator. G(s) becomes in this case:
Ã n
!
X
νi ωi2
G(s) =
− 1 Ka
(3.10)
s2 + 2ξi ωi s + ωi2
i=1
where ξi represents mode i’s damping ratio. The experimental open-loop FRF
corresponding to the active truss is shown (in dB) in Fig. 2.9c.
3.3
Static displacement
From Eq. 3.1, the elongation ∆ = bT x of the transducer can be written:
µ
¶
G(s)
f
+δ =
+1 δ
∆=
Ka
Ka
(3.11)
where G(s) is defined in Eq. 3.10. Under static conditions (s = 0) and combining
Eq. 3.10 with Eq. 3.11, one gets:
Ã n !
¯
X
¯
νi δ
(3.12)
=
∆¯
s=0
i=1
On the other hand, ∆ can also be found from Eq. 3.2, which gives:
¯
¡
¢−1
¯
bKa δ
= bT K + Ka bbT
∆¯
s=0
(3.13)
Equating Eq. 3.12 and Eq. 3.13, one finally finds:
n
X
i=1
¡
¢−1
bKa =
νi = bT K + Ka bbT
Ka
+ Ka
K∗
(3.14)
34
where K ∗ is the stiffness of the structure (without the piezo) seen from the end
points of the transducer: (K ∗ )−1 = bT (K)−1 b. Eq. 3.14 produces the following
result:
n
X
νi ≤ 1
(3.15)
i=1
which will be used in chapter 4. Together with Eq. 3.9 it also mathematically
demonstrates that the open-loop FRF G(s) is negative for s = 0, as shown in
Fig. 3.1. Thus, the alternating pole-zero patterns begins with a zero.
3.4
3.4.1
Closed-loop system
Global coordinates
The Integral Force Feedback (IFF) consists of
δ(s) =
g f (s)
Ka s
(3.16)
where g is the gain of the controller and the coefficient K1a has been introduced
for the purpose of normalisation; note that it is a positive feedback. The integral
term 1/s introduces a 90◦ phase shift in the feedback path and thus damping in
the system2 ; it also introduces a -20dB/dec slope in the open-loop FRF, and thus
reduces the risks of spillover instability.
Combining Eq. 3.1, 3.2 and 3.16, one easily gets an equation for the closed-loop
poles of the system:
¸
·
g
2
T
T
M s + (K + Ka bb ) −
(Ka bb ) x = 0
(3.17)
s+g
The asymptotic roots for g → 0 (open-loop poles) satisfy
£
¤
M s2 + K + Ka bbT x = 0
(3.18)
whose solutions are the natural frequencies of the structure ωi when the electrodes
are short-circuited (cf. §2.4.2). On the other hand, the asymptotic roots for
g → ∞, which correspond to the zeros zi of G(s), are given by the eigenvalue
problem
£
¤
M s2 + K x = 0
(3.19)
which corresponds to the situation where the axial contribution of the transducer
has been removed (Ka = 0, see §2.4.2).
2
A direct force feedback would instead artificially decrease the transducer stiffness Ka without
changing the damping (Chen, Lurie, and Wada, 1989).
3.4 Closed-loop system
3.4.2
35
Modal coordinates
IFF
b)
a)
Figure 3.2: a) Root locus of the IFF for a given structure, b) evolution of this
root locus as the zero zi moves towards the origin. Only one half of the locus is
shown; the dotted lines correspond to the maximum damping.
If one goes into modal coordinates as we did in section 2.4.3, assuming that the
structural modes are well separated, Eq. 3.17 can be reduced to a set of uncoupled
equations (Preumont, 2002):
s2 + z 2
1 + g ¡ 2 i 2¢ = 0
s s + ωi
(3.20)
Such a root locus, starting from ±jωi and ending at ±jzi , is shown in Fig. 3.2a
when zi and ωi are not too far apart. The maximum modal damping is given by:
³
ωi − zi
ωi ´
ξ max =
zi ≥
(3.21)
2zi
3
Eq. 3.21, based on the assumption of well separated modes, can be used to estimate the performances of the IFF from the knowledge of ωi and zi , obtained e.g.
from a FE model of the structure.
When the distance between zi and ωi increases, the shape of the root locus
changes as shown in Fig. 3.2b. For zi < ωi /3, the root locus touches the real
axis, which means that critical damping can be attained (ξi = 1). Finally, it can
be shown (Preumont et al., 1992) that, for small gains, the closed-loop structural
damping ratio can be approximated by:
gνi
ξi ≈
(3.22)
2ωi
36
which provides a formal justification for the placement of the active struts in the
places where νi is maximum, as suggested in §2.4.4.
3.4.3
Simplified linear analysis
Most of the studies performed on the IFF at the Active Structures Lab. (ULB)
have used, explicitly or implicitly, the assumption that the active control does
not change the mode shapes (Preumont, 2002, 2006). This simplification allows
the use of a fairly simple theory and the prediction of ξimax based on the fraction
of modal strain energy νi only.
After left and right multiplication by the matrix of modal shapes Φ (x = Φα
where α is the vector of modal amplitudes), Eq. 3.17 becomes:
h
diag(µi )s2 + diag(µi ωi2 ) −
i
g
ΦT (Ka bbT )Φ α = 0
s+g
(3.23)
where the orthogonality relations 2.31 and 2.32 have been used. The matrix
ΦT (Ka bbT )Φ is in general fully populated; with the assumption that the mode
shapes do not change, however, one has:
and
ΦT KΦ = diag(µi zi2 )
(3.24)
which, combined with the definition of νi (Eq. 2.33), gives:
ΦT (Ka bbT )Φ = diag(νi µi ωi2 )
(3.25)
zi2 = ωi2 (1 − νi )
(3.26)
and thus:
Introducing Eq. 3.26 into Eq. 3.21, one finds an expression for ξimax :
ξimax
√
νi
1 − νi − (1 − νi )
=
≈
2(1 − νi )
4(1 − νi )
(3.27)
which stresses the importance of the ratio of modal strain energy νi in the performances of the IFF.
The assumption of unchanged mode shapes is fairly restrictive and must be used
with caution. Its validity (in particular, that of Eq. 3.26 and Eq. 3.27) was
studied by Bossens (2001) for active tendon (cable) structures; he found that, on
this type of structure, the assumption generally produces accurate results. Its
accuracy in the case of truss structures is investigated in §3.5.1.
3.5 Application to the truss
3.5
3.5.1
37
Application to the truss
Numerical verifications
This section numerically compares three different ways to predict the performances, from the easiest to the most involved:
• (1) zi and the maximum structural damping ratio ξimax are estimated by
means of the computed ωi and νi (Table 2.3) and of the approximate
formulae (3.26) and (3.27). This method is based on the assumption of
unchanged mode shapes (§3.4.3)
• (2) zi is directly computed with the specific FE model (SAMCEF), by
removing the axial stiffness of the transducer. ξimax is estimated with formula 3.21, which is exact for a single-mode structure and does not use
νi . This method relies on the less restrictive assumption of well separated
modes (§3.4.2).
• (3) The maximum structural damping ratio ξi is directly evaluated by
means of the full MATLAB model. The comparison with (2) gives
an idea of the influence of the modal coupling.
We analyze the active damping of modes 1 and 2, using the two piezoelectric
struts (one at a time, but not simultaneously).
Table 3.1 compares the values of zi obtained with methods (1) and (2), when
either strut 1 or strut 2 is active. The approximate equation (3.26) produces very
large errors, because the mode shapes are drastically different after removing the
axial stiffness of the strut. Although the map of fraction of modal strain energy
νi constitutes an excellent guide for actuator location, it clearly fails in providing
quantitative estimation of the active control performances. Eq. 3.26 does not
apply for this type of structures.
strut 1
strut 2
mode
1
2
1
2
zi /2π
(1)
(2)
18.62 2.02
22.50 22.35
18.79 4.07
21.83 19.44
Table 3.1: Predicted zi (in Hz ); (1) approximate formula 3.26, and (2) removing
the axial stiffness Ka in the FE model.
Table 3.2 gives the maximum modal damping ξi predicted for the two active struts
and IFF active control. “Critical” means that ξi > 1. The explanation for these
very large damping values is as follows: because of the particular design of the
38
strut 1
strut 2
mode
1
2
1
2
(1)
0.77
0.04
0.33
1.57
IFF (Voltage)
(2)
(3)
critical critical
0.38
0.39
1.36
1.36
critical critical
Table 3.2: Predicted maximum modal damping ξi (in %) for the IFF with voltage
control; (1) approximate formulae, (2) specific FE model, (3) full MATLAB
model.
truss, removing the axial stiffness of the actuator almost produces a mechanism,
which corresponds to one zero pair (z1 or z2 ) being very close to the origin.
3.5.2
Root locus
Fig. 3.3 shows two root loci of the closed-loop system, obtained with the full
MATLAB model. When strut 1 is active (Fig. 3.3a), the loop relative to mode 2
can hardly be seen, because mode 2 is almost uncontrollable from strut 1 (ν2 is
close to 0). The vicinity of ω2 has been enlarged. Examining the root locus for
strut 2 (Fig. 3.3b), one sees that, due to the weak controllability of mode 1 from
strut 2, there is a permutation in the zeros z1 and z2 : the pole at ω2 goes to the
low frequency zero while the loop of mode 1 moves towards the zero z1 with a
slightly higher frequency.
!2
(a)
(b)
25
25
0.6
0.6
0.45
0.75
2nd mode
z2
0.3
0.45
0.15
!2
0.75
z1
!1
20
!1
0.85
0.85
15
15
first mode
10
10
0.95
0.95
5
5
z2
z1
-25
Im=2ù
-20
-15
-10
Re=2ù
-5
0
0
-25
-20
-15
-10
-5
0
0
Re=2ù
Figure 3.3: Numerical root loci of the IFF with voltage control; (a) control on
strut 1, (b) control on strut 2. The frequencies are given in Hz.
3.6 Experimental results
39
0.6
0.45
0.15
0.3
25
0.75
0.85
15
Im (Hz)
20
10
0.95
5
-25
-20
-15
-10
-5
Real (Hz)
Figure 3.4: Experimentally identified root locus of the IFF when strut 1 is active.
Each dot represents a different gain.
3.6
Experimental results
The experimental setup consisted of a B&K 2635 charge amplifier (for the force
sensor), a Dspace 1103 controller board (implementing the control law) and a
home-made voltage amplifier that drove the piezo. To avoid the saturation of the
transducer, the control law (3.16) was slightly modified according to:
g
gs
→
Ka s
Ka (s + β)2
(3.28)
with β much lower than the first natural frequency of the structure. This modification was found to be more effective than the one used previously [g/Ka (s + β)]
as it has a true zero at the origin; it also slightly improves the behavior of the active truss at low frequency, see §3.8. In practice, the force sensor also introduces
a high-pass filter in the system (via its charge amplifier) with a corner frequency
at 0.2 Hz, which is low enough, compared with the first natural frequency of the
system, to be neglected.
The control system was implemented on strut 1; Fig. 3.4 shows the evolution
of the closed-loop poles when g increases from 0 to +∞. Each dot represents a
different measurement, and the solid line corresponds to simulation results (it is
again that of Fig. 3.3a). Critical damping could be attained.
The frequency response F1 /V2 has been measured with a HP 35670A Fourier
analyzer; it is shown in Fig. 3.5, with a gain g leading to ξ1 ≈ 60%.
40
dB
-20
Open loop
-40
-60
-80
With control
10
Freq. (Hz)
100
Figure 3.5: Experimental FRF F1 /V2 with and without the active control on
strut 1 (the control gain is such that ξ1 ≈ 60%).
3.7
Charge (current) control
Charge (or current) control is known to substantially decrease the hysteresis
of piezoelectric actuators (Comstock, 1981; Newcomb and Flinn, 1982). Quasistatic actuation with charge control (e.g. for precise positioning of a device)
presents some practical difficulties, mainly because of the unavoidable presence
of small bias currents that cause the DC loading of the load capacitance (Main
et al., 1995) and, ultimately, can lead to the saturation of the charge amplifier.
Dynamic actuation, on the other hand, allows the use of a high-pass filter that
prevents such issues; practical realizations have been presented in the literature,
e.g. by Dörlemann et al. (2002).
When a current source is used, the system is governed by Eq. 2.29 instead of
Eq. 3.2:
Ka
Ka
M ẍ + (K +
bbT )x = b
δ∗
(3.29)
2
1−k
1 − k2
with δ ∗ , nd33 Q/C the free piezoelectric expansion when charge control (instead
of voltage control) is used. Eq. 3.29 is very similar to Eq. 3.2, except that the
transducer has an increased stiffness Ka /(1 − k 2 ), corresponding to open electrodes.
Using the same force feedback as in the “voltage control” case (IFF on Q, which
amounts to proportional feedback on I), and after modifying slightly Eq. 3.1 and
Eq. 3.16 to account for the increased stiffness of the transducer, one easily finds
3.7 Charge (current) control
41
dB
Electrical Impedance V1 / I 1
!1
18
18.2
18.4
Ò1
f 1 /V1
f1/ I 1
!1
Ò1
18.6
18.8
19
19.2
19.4
19.6
19.8
20
Freq. (Hz)
Figure 3.6: Experimental open-loop FRF: f1 /V1 , f1 /I1 and the electrical
impedance of strut 1 V1 /I1 (the curves have different scales along the Y −axis).
that the closed-loop poles satisfy the eigenvalue problem:
·
µ
¶
¸
Ka
Ka
g
2
T
T
Ms + K +
bb
−
bb x = 0
1 − k2
s + g 1 − k2
(3.30)
The asymptotic roots for g = 0 satisfy Eq. 2.30; its solutions are the natural
frequencies of the global structure, Ωi , when the transducer electrodes are open.
On the other hand, the asymptotic roots when g → ∞ are again solutions zi of
the eigenvalue problem Eq. 2.27 (Ka = 0).
Eq. 3.30 can be transformed into independent modal coordinates; it becomes
1+g
s2 + zi2
=0
s(s2 + Ω2i )
(3.31)
(i = 1, . . . , n) which is the same as Eq. 3.20, except that the natural frequencies
Ωi (open electrodes) are used instead of ωi (short-circuited electrodes). The root
locus again has the shape of Fig. 3.2, and the maximum damping ratio is given by
Eq. 3.21 with Ωi instead of ωi . As the ωi are very close to the Ωi (see Table 2.3),
both methods lead to approximately the same damping ξi .
Fig. 3.6 presents a zoom on the experimental FRFs f1 /V1 (voltage control) and
f1 /I1 (current control): the slight increase in natural frequency (from ω1 to
Ω1 ) is visible. The third curve is the electrical impedance V1 /I1 of the strut:
42
F
x
dB
X
F
m
H(s)
K
Ka V
1
K+Ka
1
K
Frequency
(a)
(b)
Figure 3.7: a) 1-d.o.f. piezoelectric structure with force feedback; b) structural
response X/F without (plain) and with (dashed) IFF control.
anticipating on the results of the next chapter, this curve has resonances at Ωi
and anti-resonances at ωi , which can also be seen in the figure.
3.8
Softening of the active struts
The very wide loop of the root locus shown in Fig. 3.4 could suggest that the
IFF is a ‘miracle’ solution, with an incredible damping capability. Actually, this
damping capability is counterbalanced by a few drawbacks. The main one consists
in the static softening of the active struts when the control is on; this problematic
has been analyzed e.g. by Bossens (2001) or Ehmann et al. (2002). Consider the
single-d.o.f. piezoelectric structure of Fig. 3.7a: it consists of a piezo transducer
of stiffness Ka with a collocated load cell; a spring of stiffness K is placed in
parallel. Applying the usual equations, the displacement X(s) of the mass when
an external force F (s) is applied is found to be:
·
¸−1
X
Ka
2
= ms + K +
(3.32)
F
1 + Ka H(s)
where m is the structural mass and H(s) the transfer function of the controller.
Without controller (H(s) = 0), the static response is:
¯
1
X ¯¯
=
(3.33)
¯
F s=0 K + Ka
When the IFF is implemented, i.e. H(s) = g/s, Eq. 3.32 becomes:
·
¸−1
s
X
2
= ms + K + Ka
F
s+g
(3.34)
and the static response X/F |s=0 is given by 1/K: at low frequencies, the Integral
Force Feedback thus effectively cancels the stiffness of the active strut. This result
3.8 Softening of the active struts
43
X/F (dB)
-40
IFF only
-60
IFF + HP filter (2Hz)
-80
Open-Loop
F
-100
strut 2
X
-120
strut 1
0.1
1
Frequency (Hz)
10
100
Figure 3.8: Response X of the top of the truss to a perturbation F , first with
a simple IFF controller, then with an IFF in series with a 2nd order High-Pass
(HP) filter.
is illustrated in Fig. 3.7b, which shows the FRFs corresponding to the structure of
Fig. 3.7a with and without control: the damping of the structural mode is indeed
enhanced (dashed curve), but the response to low-frequency perturbations (below
the resonance) is larger. The trade-off between static amplification and damping
immediately appears: a small ratio Ka /K leads to a small static amplification,
but it also decreases the attainable damping, which is governed by the fraction
Ka
.
of modal strain energy νi : in this case, νi = K+K
a
On real, 3-dimensional structures, the impact of this softening depends heavily
on the respective positions of the perturbation and of the sensor. For example,
the softening cannot be seen with the present setup when the perturbation comes
from strut 1 or 2: see e.g. Fig. 3.5. On the other hand, it can be seen with other
excitation sources: Fig. 3.8 shows a simulation when a point force perturbation
is applied at the top of the truss. The static response is increased by 40dB when
the IFF is switched on!
There are no evident solutions to this softening issue. H(s) can be modified
in such a way that the low-frequency part of the signal is not integrated: an
example is provided by Eq. 3.28, which introduces a High-Pass (HP) filter in
series with the IFF. Fig. 3.8 presents the response of the truss with such a filter
(2nd order, ωc =2Hz). Although HP filters indeed improve the situation, they
do not completely solve the issue (in Fig. 3.8 the amplification still reaches 20dB
around [2-8] Hz); they are also detrimental to the damping performances. Bossens
(2001) proposed the use of a feedforward controller in parallel to the IFF, but this
method relies on the availability of a signal correlated to the perturbation (see
44
References
e.g. Fuller et al., 1996). Ehmann et al. (2002) have experimentally compared on
a truss the IFF vs. more elaborate (model-based) controllers. These controllers
could introduce as much damping as the IFF without introducing any static
amplification; they are however more difficult to design, and they rely on a model
of the structure, which implies other robustness issues.
3.9
References
F. Bossens. Amortissement actif des structures câblées: de la théorie à
l’implémentation. PhD thesis, Université Libre de Bruxelles, 2001.
paper 89-1327 CP, 1989.
R.H. Comstock. Charge control of piezoelectric actuators to reduce hysteresis
effects. Us patent 4,263,527, 1981.
C. Dörlemann, P. Muß, M. Schugt, and R. Uhlenbrock. New high speed current
controled amplifier for pzt multilayer stack actuators. In Actuator02, Bremen,
Germany, 2002.
C. Ehmann, U. Schönhoff, and R. Nordmann. Robust controller synthesis vs.
integral force feedback with collocation for active damping of flexible structures.
In Proc. ISMA 2002, Leuven, Belgium, 2002.
C.R. Fuller, S.J. Elliott, and P.A. Nelson. Active Control of Vibration. Academic
Press, 1996.
J.A. Main, E. Garcia, and D.V. Newton. Precision position control of piezoelectric
actuators using charge feedback. J. of Guidance, Control and Dynamics, 18
(5):1068–1073, Sept.-Oct. 1995.
C.V. Newcomb and I. Flinn. Improving the linearity of piezoelectric ceramic
actuators. Electronics Letters, 18(11):442–443, 1982.
2002. 2nd edition.
Chapter 4
Passive shunt damping
Shunt damping techniques exploit the capability of piezoelectric materials to
transform mechanical (strain) energy into electrical energy, which is then dissipated in the electrical circuit. The conversion capability depends very much on
(i) the ability to concentrate the strain energy into the active material (the piezo)
and (ii) the capability of the piezoelectric transducer to transform this strain energy into electrical energy. The former depends on the fraction of modal strain
energy νi (Eq. 2.33), and the latter on the material electromechanical coupling
factor k 2 (Eq. 2.17).
This chapter describes the behavior of structures with passive resistive (R) and
resistive-inductive (RL) shunts. Closed-form formulae for the maximum attainable damping and optimum values of the electrical components are provided;
these analytical formulae are numerically validated on the FE model of the truss.
Experimental results will be presented in chapter 5, along with those of the negative capacitance shunt.
4.1
4.1.1
Introduction
Classical shunts
The apparent simplicity of piezoelectric shunt damping is appealing and has motivated a huge amount of research within the structural control community. The
first demonstration of the concept to be reported in the literature was performed
by Forward (1979) with an inductive (L) shunt: he presented qualitative physical
justifications and experimental results1 .
1
The work of Edwards and Miyakawa (1980) on the concept is also sometimes cited but their
report has not been published in the literature and could not be found for this thesis.
45
46
Cp
L
a
b
c
d
e
f
Figure 4.1: Various passive shunts proposed in the literature: a) resistive; b) series
RL; c) parallel RL; d) series RL with a parallel capacitance Cp ; e) multimode
shunt damping (Hollkamp); f) multimode shunt damping (Wu)
Some ten years later, Hagood and von Flotow (1991) published a thorough theoretical formulation. They considered that a shunted piezoelement behaves like
a visco-elastic material with frequency-dependent stiffness and loss factor: they
provided analytical formulae for resistive (R) and inductive-resistive (RL) shunting, Fig. 4.1a-b. The interaction of the piezo with a single-mode structure was
also considered and optimal values for R and L were given. Their in-depth discussion triggered research on the subject in many research departments: see e.g.
Edberg et al. (1992) or Davis and Lesieutre (1995).
Wu proposed to connect the resistor and the inductor in parallel rather than in
series (Fig. 4.1c); it was shown by Caruso (2001) that the performances are very
similar to that of a series shunt. Extension to multi-mode damping has been
considered by Hollkamp (1994), which used several RLC circuits connected in
parallel (Fig. 4.1e), and by Wu (1998), which used current-blocking parallel LC
circuits placed as in Fig. 4.1f (his technique is more effective than Hollkamp’s but
it requires more electrical components).
RL circuits require high values for the inductance L (typically hundreds or even
thousands of Henries), which is an issue because of the practical impossibility
of manufacturing such inductors within acceptable space and weight constraints.
This problem can be partly overcome by using an electronic circuit (gyrator)
that simulates the behavior of an inductance, see Fig. 4.2 (Antoniou, 1969). The
value of L that can be attained with these circuits is much larger (up to thousands
of Henries, although the implementation can be problematic for these extreme
values); it however requires the presence of a power source. Park and Inman
(2003) proposed to connect a capacitor Cp in parallel to the shunt (Fig. 4.1d): this
4.1 Introduction
47
I
R1
I
R2
R5
R2
R3
R3
V
R1
C4
R5
V
C4
a)
L=
R1R3R5C4
R2
b)
Figure 4.2: Electronic circuits (gyrators) made of operational amplifiers that
simulate the behavior of an inductance: a) Riordan circuit; b) Antoniou circuit
configuration reduces the required value of L, but it also decreases the attainable
damping as demonstrated in Caruso (2001). A negative capacitance, by contrast,
increases the performances: it is the subject of the next chapter.
4.1.2
Alternative shunts
The original idea of a simple passive R or RL shunt circuit has evolved in a wide
variety of concepts. These concepts can be classed into different categories:
• Adaptive shunts: The damping performances of the RL shunts (whether
single-mode or multi-modes) are extremely sensitive to the tuning of the
shunt on the targeted structural natural frequencies. Some researchers
(e.g. Rew and Lee, 2001) proposed the use of adaptive circuits that are
able to compensate for a drift of the system characteristics. These algorithms are generally based on the RMS minimization of a signal and their
convergence has been reported to be quite slow (Niederberger, 2005). A different technique, based on the minimization of the relative phase between
two signals, has been presented by Niederberger et al. (2004), apparently
with better results.
• Active shunts2 : Shunt damping is not limited to passive circuits. Active
circuits simulating the behavior of a negative capacitance were proposed
2
Strictly speaking, the RL shunt is also “active” when it is implemented with gyrator circuits, because of the required power source. There are however few stability issues because the
implementation simulates the behavior of a passive circuit.
48
as early as 1979 and are presented in the next chapter; they are shown
to enhance the electromechanical coupling between the structure and the
circuit. Other researchers employed optimal control theory (e.g. LQR) to
design circuits that minimize the H2 or H∞ norm of a signal. Besides,
researchers such as Tang and Wang (2001) investigated the use of hybrid
circuits, in which a piezo transducer is simultaneously shunted passively
and embedded in an active control scheme.
• Nonlinear shunts: this category mainly concerns the so-called ‘switching’
shunts, in which the piezo is briefly connected to a passive (R or RL) or
active electric circuit, keeping it disconnected most of the time. Typically,
these connections occur at a maximum and/or a minimum of the structural
modal amplitude; they change the piezo’s stiffness and discharge the energy
accumulated in the transducer (Clark, 2000; Holnusen and Cunefare, 2003;
Guyomar and Richard, 2005). The main advantage of this method comes
from its insensitivity to drifts of structural characteristics (the added damping does not depend on a precise tuning of the shunt on a targeted natural
frequency); its main difficulty, which has not been completely solved to this
date, consists in determining the extremum of the modal amplitude: it is
not easy for multi-mode structures, and out-of-time switching can potentially excite high-frequency modes.
• Distributed shunts: In this technique a structure is covered with regularly spaced piezo transducers which are connected to a general electric
network with as many input pins as the number of transducers (e.g. Maurini et al. 2004); if we refer to an active control terminology, this technique
can be considered as “centralized”, in contrast to the previous techniques
which are “decentralized” (each piezo is connected to a single, independent electric circuit). The challenge of course consists in finding an electric
circuit simple enough to be implemented. Bisegna et al. (2006) have had
some success with a beam, using a periodic circuit made up of parallel RL
elements that was shown to enhance the damping of the first five modes
(these results are also reported in two PhD theses: Maurini, 2005 and Porfiri, 2005). Things are however much more complicated for plates, because
it is no longer a 1D problem, and, to this date, the circuits that have been
proposed still involve transformers, which is not very practical (Alessandroni et al., 2005). Distributed shunts can also be advantageous when the
structure is periodic, such as bladed discs in turbomachinery; see e.g. Yu
and Wang (2007) and the references therein.
To conclude this section, let us point out that all these techniques are very closely
related to those used in energy-harvesting, in which the ambiant vibration
4.2 Electrical admittance of the structure
49
(a)
(b)
k2 =
x
M
dB
sC
I
V
z 2àp 2
z2
p
I
V
z
sC(1 à k 2)
!
Transducer
þ
ù
Figure 4.3: a) Elementary dynamical model of the piezoelectric stack transducer.
b) Typical admittance FRF of the transducer, in the vicinity of its natural frequency.
energy of the structure that is extracted is not dissipated but stored and used to
power other electronic devices (typically MEMS), see e.g. Lesieutre et al. (2004)
or Guyomar and Richard (2005).
4.2
4.2.1
Electrical admittance of the structure
Single-mode structure
It was stressed in chapter 2 that the stiffness and capacitance of a piezoelectric
transducer depend on the electrical and mechanical boundary conditions. The
Ka
piezo is stiffer when open-circuited (with Ka → 1−k
2 ), and its capacitance is lower
S
when it is mechanically blocked (with C → C = C(1 − k 2 )). This behavior can
be detected in the electrical admittance curve of the transducer.
Consider the system of Fig. 4.3a, which is the simplest possible dynamical model
of a piezoelectric stack transducer; assuming that the transducer mass M is
lumped at the top and using the equations of §2.4.1, one finds that the system
obeys:
(M s2 + Ka )x = Ka nd33 V
£
¤
s C(1 − k 2 )V + nd33 Ka x = I
(4.1)
(4.2)
which are identical to Eq. 2.25 and Eq. 2.26, but this time M and K are scalar
quantities. Eliminating x between both equations and using Eq. 2.17 that defines
the electromechanical coupling factor k 2 , we obtain the electrical admittance Y (s)
50
(inverse of the impedance Z(s)):
¸
·
I(s)
M s2 + Ka /(1 − k 2 )
2
Y (s) =
= sC(1 − k )
V (s)
M s2 + Ka
(4.3)
This admittance curve is shown in Fig. 4.3b. For ω → 0 it is that of a capacitor
of value C, and for ω → ∞ it is that of a capacitor of value C S = C(1 − k 2 ). In
between the denominator vanishes at the transmission poles (±jp) with
p2 =
Ka
M
(4.4)
and the numerator vanishes at the transmission zeros (±jz) with
z2 =
Ka /(1 − k 2 )
M
(4.5)
p is the natural frequency with short-circuited electrodes, and z is the natural frequency with open electrodes. This was expected since I = 0 when the electrodes
are open and V = 0 when they are short-circuited. One also finds that
z 2 − p2
= k2
z2
(4.6)
which constitutes a practical way to determine the electromechanical coupling
factor from admittance (or impedance) FRF measurements. Eq. 4.6 is only valid
for piezoelectric stack transducers, whose first mode shape is very similar to
that of the structure modelled in Fig. 4.3a. Other kinds of transducers, such
as piezoelectric patches, rings or monocrystals have different mode shapes, and
Eq. 4.6 must be adapted. Formulae corresponding to different transducer shapes
can be found on most producers’ web sites, e.g. Morgan Electro Ceramics or
NEC-Tokin.
4.2.2
Multi-mode structure
The admittance curve of a piezo transducer inserted into a mechanical structure
is similar to that described in the last section, but many more modes appear in
the curve. Introducing the modal expansion of x (Eq. 3.6) into Eq. 2.26 one gets:
( n
)
X bT φi φT b
2
i
Q = C(1 − k )V + nd33 Ka
nd33 Ka V
(4.7)
µ (ω 2 + s2 )
i=1 i i
or
n
X
νi
Ystruct
Q
=
= C(1 − k 2 ) + Ck 2
V
s
1 + s2 /ωi2
i=1
(4.8)
4.2 Electrical admittance of the structure
51
Q
V
Q
V
S
2
C =C(1-k )
Cstatic
Ci1
0
Freq.
0
a)
Ci2
!i
Òi
Freq
b)
Figure 4.4: (a) Capacitance Q/V of a piezoelectric transducer embedded in a
fictitious 3-mode structure; (b) the approximation around ωi if the modal density
is low.
which uses the definition of the fraction of modal strain energy νi (Eq. 2.33) and
that of the transducer coupling factor k 2 (Eq. 2.17); Ystruct (s) is defined as the
electrical admittance of the piezoelectric structure, seen from the electrodes.
Q/V can be regarded as the “dynamic” capacitance of the system; it is shown
in Fig. 4.4a for a fictitious undamped three-mode structure. Because the piezoelectric structure, seen from its electrodes, is passive, its admittance exhibits
alternating poles and zeros; mathematically, this occurs because all the residues
(the νi in Eq. 4.8) are positive. The poles of Eq. 4.8 are at ωi , the natural frequencies of the structure with short-circuited electrodes. The zeros, on the other
hand, are the solution of Eq. 2.26 with Q = 0:
0 = C(1 − k 2 )V + nd33 Ka bT x
(4.9)
Eliminating V between Eq. 4.9 and Eq. 2.25 and using the definition of k 2
Eq. 2.17, it is found that the zeros are solutions of
µ
¶
Ka
2
T
Ms + K +
bb
x=0
(4.10)
1 − k2
This equation is identical to Eq. 2.30, indicating that the zeros of the admittance
are the poles of the system when the transducer electrodes are left open, Ωi . Thus,
52
in a single admittance (or impedance) measurement, the open and short-circuit
natural frequencies Ωi and ωi can be determined. This result has been experimentally demonstrated in Fig. 3.6; it remains valid even if other types of piezoelectric
transducers (e.g. d31 patches) are used instead of d33 stacks.
When ω → ∞, the capacitance tends to C S = C(1 − k 2 ), i.e. the constant-strain
capacitance of the transducer, and at very low frequencies Eq. 4.8 gives:
³
X ´
Q(s)
(4.11)
Cstatic , lim
= C 1 − k2 + k2
νi
s→0 V (s)
Introducing Eq. 3.14 into Eq. 4.11, one gets:
µ
Cstatic = C 1 − k 2 + k 2
Ka
Ka + K ∗
¶
(4.12)
where K ∗ once again represents the stiffness of the structure (without the piezo)
seen from the end points of the transducer: (K ∗ )−1 = bT (K)−1 b. The static
capacitance is the only value that can be measured once the piezo element is
embedded in a structure, because C is no longer accessible. If K ∗ = 0, Cstatic
equals C; on the other hand, if K ∗ → ∞, one has Cstatic → C(1 − k 2 ) = C S .
Note that Fig. 4.4a has been exaggerated for the purpose of illustration; in practice the parameters Ck 2 νi are very small and the ωi are extremely close to the
Ωi . Note also that all these equations have been written assuming a constant
permittivity εT3 ; it was found in practice that the permittivity of a PZT sample
decreases by approximately 2% per decade: the horizontal parts of the curve in
Fig. 4.4a have a slight decreasing slope.
4.2.3
Generalized electromechanical coupling factor
Eq. 4.6 defines the material coupling factor k 2 from the open-circuit and shortcircuit natural frequencies of the transducer; it can be generalized for a structural
mode i by:
Ω2 − ω 2
(4.13)
Ki2 = i 2 i
Ωi
Ki is the generalized electromechanical coupling factor; it combines material data
with information about the structure. The next sections show that the performances of the passive shunts are closely related to Ki . Note that, for small k and
νi , the usual assumption of unchanged mode shapes applies, and one has:
and
ΦT (K +
Ka
bbT )Φ ≈ diag(µi Ω2i )
1 − k2
(4.14)
4.3 Damping performances
53
which, combined with the definition of νi (Eq. 2.33), gives:
³
k 2 νi ´
Ω2i ≈ ωi2 1 +
1 − k2
and thus:
Ki2 ≈
k 2 νi
1 − k 2 + k 2 νi
(4.15)
(4.16)
which points out the influence of the fraction of modal strain energy νi and of
the electromechanical coupling factor k 2 on passive damping performances. Ki
is easily computed by successively adapting the electrical boundary conditions in
the FE model of the structure and can thus be used as a performance index in
an optimisation process. Note that, in the literature, the definition
Ki2 =
Ω2i − ωi2
k 2 νi
≈
2
1 − k2
ωi
(4.17)
is often used instead of Eq. 4.13. The difference between the two definitions is
insignificant in most practical applications, but Eq. 4.17 does not supply Ki = k
if νi = 1.
4.3
Damping performances
This section describes the structural behavior with R and RL shunts; in particular, closed-form solutions for the maximum attainable damping ratios ξi and for
the optimum values of the shunt components are provided. These formulae are
numerically evaluated in §4.4; experimental results are presented in chapter 5,
along with those of the negative capacitance shunt.
The performance of a shunt circuit can be optimized in many different ways. One
popular method consists in choosing R and L such that the H∞ norm3 of a chosen
structural FRF is minimized. Such an approach was developed e.g. by Hagood
and von Flotow (1991); it is not particularly easy and the results depend on
the chosen FRF, i.e. on the position of the perturbation and on the point whose
displacement is minimized.
Another possibility consists in maximizing the damping ratio of a targeted mode,
so as to maximize its decay rate (see chapter 1) and thus decrease the structural
sensitivity to a perturbation (shock etc.). Such a methodology was used e.g.
by Caruso (2001); it is also the one used in this work. Note that the results
produced by the various techniques are quite close to each other.
3
n
i.e., the parameter
o
max |H(jω)|
ω
where H(jω) is the chosen FRF.
54
4.3.1
Eigenvalue problem
Consider the electrical admittance of a piezoelectric structure Ystruct (s), defined
in Eq. 4.8 and shown in Fig. 4.4a for a fictitious 3-mode structure. If the modal
density around ωi is low, Eq. 4.8 can be approximated around ωi by:


2ν ω2
X
k
i i
νj 
(4.18)
Ystruct (s) ≈ sC 1 − k 2 + 2
+ k2
s + ωi2
j>i
which is shown in Fig. 4.4b. The coefficients Ci1 and Ci2 defined in the figure are
readily identified as:


X
Ci2 = C 1 − k 2 + k 2
(4.19)
νj 
and
Ci1 = Ci2 + Ck 2 νi
j>i
and Eq. 4.18 can be rewritten as:
Ystruct (s) ≈ sCi2 + sCk 2
νi ωi2
s2 + ωi2
(4.20)
It was demonstrated in §4.2.2 that the open-circuit natural frequencies Ωi are the
zeros of the admittance Ystruct (s); from Eq. 4.20, the Ωi can thus be approximated
by:
µ
¶
Ci1 2
Ck 2 νi
2
Ωi ≈
ω = 1+
ωi2
(4.21)
Ci2 i
Ci2
Unlike Eq. 4.15, Eq. 4.21 is based only on the assumption of well separated modes.
Note that Eq. 4.21 reduces to Eq. 4.15 in the case of a single-mode structure; in
this case the coefficients Ci1 and Ci2 also reduce to Cstatic (defined in Eq. 4.11)
and C S = C(1 − k 2 ), respectively.
When an electrical shunt of admittance Yshunt (s) is connected to the piezo, the
total admittance of the shunted structure is classically given by:
Ytot (s) = Ystruct (s) + Yshunt (s)
(4.22)
From the electrical network theory, the poles of the shunted structure are given
by the zeros of the total admittance Ytot (s); this result is also demonstrated in
chapter 5, §5.3. From Eq. 4.20, the ith pole of a piezoelectric structure shunted
by a general admittance is thus given by the characteristic equation:
Ytot (s) ≈ Yshunt (s) + sCi2 + sC
k 2 νi ωi2
=0
s2 + ωi2
(4.23)
which leads to Eq. 4.21 and to Ωi when Yshunt → 0, and to ωi when Yshunt → ∞.
55
Òi
!i
Òi !i
!i
Figure 4.5: Root locus plot for resistive shunting (only the upper half is shown).
4.3.2
R shunt
If Yshunt = 1/R, Eq. 4.23 becomes:
1
k 2 νi ωi2
+ sCi2 + sC 2
=0
R
s + ωi2
(4.24)
which can be rearranged into:
1+
s2 + ωi2
1
=0
RCi2 s(s2 + Ω2i )
(4.25)
where Eq. 4.21 has been used. The root locus of Eq. 4.25 is identical to the locus
of the IFF (Eq. 3.20); it is shown once again in Fig. 4.5. The poles are in this
case at ±jΩi (open electrodes) and the zeros are at ±jωi (short-circuit). Just as
with the IFF, the maximum achievable damping is given by
max
ξi,R
=
Ω2 − ω 2
Ωi − ωi
K2
' i 2i = i
2 ωi
4
4 Ωi
(4.26)
and it is obtained for (Preumont, 2002):
1
=
RCi2
r
Ωi
Ωi
ωi
(4.27)
The fact that the Integral Force Feedback and the resistive shunting share a
similar root locus is an interesting feature. Despite this similarity, they have very
different performances.
56
4.3.3
Series RL shunt
In the case of a series RL shunt, one has:
Yshunt (s) =
1
Ls + R
(4.28)
and Eq. 4.23 becomes:
1
k 2 νi ωi2
+ sCi2 + sC 2
=0
R + Ls
s + ωi2
or:
R
s + s3 +
L
µ
1
4
Ci2 L
¶
+
Ω2i
s2 +
(4.29)
R 2
ω2
Ωi s + i = 0
L
Ci2 L
(4.30)
where Eq. 4.21 has been used. One can define the electrical frequency and damping by:
ωe2 =
1
LCi2
2ξe ωe =
R
L
(4.31)
and Eq. 4.30 becomes
¡
¢
s4 + 2ξe ωe s3 + ωe2 + Ω2i s2 + 2ξe ωe Ω2i s + ωi2 ωe2 = 0
(4.32)
which can be rearranged in a root locus form:
1 + 2ξe ωe
s(s2 + Ω2i )
=0
s4 + (Ω2i + ωe2 )s2 + ωi2 ωe2
(4.33)
In this formulation, 2ξe ωe plays the role of the gain in a classical root locus. For
large R, the poles tend to ±jΩi , as expected. For R = 0 (i.e. ξe = 0), they are
the solutions p1 and p2 of the characteristic equation s4 + (Ω2i + ωe2 )s2 + ωi2 ωe2 = 0
which accounts for the classical double peak of resonant dampers, with p1 above
jΩi and p2 below jΩi . Fig. 4.6 shows the root locus for a fixed value of ωi /Ωi
and various values of the electrical tuning, expressed by the ratio
αe =
ωe ωi
Ω2i
(4.34)
The locus consists of two loops, starting respectively from p1 and p2 ; one of them
goes to jΩi and the other goes to the real axis, near −Ωi . If αe > 1 [Fig. 4.6(a)],
the upper loop starting from p1 goes to the real axis, and that starting from p2
goes to jΩi , and the upper pole is always more heavily damped than the lower
one (note that, if ωe → ∞, p1 → ∞ and p2 → jωi , the lower branch of the root
locus becomes that of the resistive shunting). The opposite situation occurs if
57
p1
(a)
p1
(b)
ëe < 1
ëe > 1
jÒ i
j!i
p2
jÒ i
j!i
p2
Resistive
shunting
à Òi
à Òi
Im(s)
p1
(d)
(c)
ëe = 1
jÒ i
j!i
Q
jÒ i
Q
p2
Optimal
Damping
à Òi
à Òi
Re(s)
Figure 4.6: Root locus plot for inductive shunting (only the upper half is shown).
The maximum modal damping at Q is ξi = Ki /2.
αe < 1 [Fig. 4.6(b)]: the upper loop goes from p1 to jΩi and the lower one goes
from p2 to the real axis; the lower pole is always more heavily damped. If αe = 1
[Fig. 4.6(c)], the two poles are always equally damped until the two branches
touch each other in Q. This double root is achieved for
αe =
ωe ωi
=1
Ω2i
and
ξe2 = 1 −
ωi2
Ω2i
(4.35)
This can be regarded as the optimum tuning of the inductive shunting. The
corresponding eigenvalues satisfy
s2 + Ω2i + Ωi (
Ω2i
− 1)1/2 s = 0
ωi2
(4.36)
For various values of ωi /Ωi (or Ki ), the optimum poles at Q move along a circle
58
of radius Ωi [Fig. 4.6(d)]. The corresponding damping ratio can be obtained
easily by identifying the previous equation with the classical form of the damped
oscillator, s2 + 2ξi Ωi s + Ω2i = 0, leading to
s
1
ξi =
2
4.3.4
Ω2i − ωi2
Ki
≈
2
2
ωi
(4.37)
Parallel RL shunt
The same methodology applied on a parallel RL shunt (instead of a series one)
leads to very similar results and conclusions. The shunt admittance is:
Yshunt (s) =
R + Ls
RLs
(4.38)
and Eq. 4.23 becomes:
¡
¢
s4 + 2ξe∗ ωe∗ s3 + ωe∗2 + Ω2i s + 2ξe∗ ωe∗ ωi2 s + ωi2 ωe∗2 = 0
(4.39)
where the new electrical frequency and damping have been defined as:
ωe∗2 =
1
LCi2
2ξe∗ ωe∗ =
1
RCi2
(4.40)
Eq. 4.39 can be rearranged in a root locus form:
1 + 2ξe∗ ωe∗
s(s2 + ωi2 )
=0
s4 + (Ω2i + ωe∗2 )s2 + ωi2 ωe∗2
(4.41)
which is very similar to Eq. 4.33. Once again two poles p1 and p2 are present,
and once again a double root can be achieved for specific values of ωe∗ and ξe∗ ;
these values are:
ωe∗ = ωi
and
ξe∗2 =
Ω2i − ωi2
ωi2
(4.42)
and the maximum attainable damping with a parallel RL shunt is:
s
1
ξi =
2
Ω2i − ωi2
Ki
=
2
Ω2i
(4.43)
4.3.5
59
Sensitivity
The damping obtained with a parallel or series RL shunt is significantly higher
than that achieved with a R shunt: the values given by Eq. 4.37 and Eq. 4.43 are
approximately the square-root of that in Eq. 4.26. Note, however, that it is much
more sensitive to the tuning of the electrical parameters on the targeted modes.
This is illustrated in Fig. 4.7, which displays the evolution of the damping ratio
of the two pairs of poles p1 and p2 when the actual natural frequency ωi0 moves
away from the nominal frequency ωi for which the shunt has been optimized (the
damping ratio associated with p1 and p2 is shown in dotted lines; the ratio ωi0 /Ω0i
is kept constant in all cases).
øi
0.3
p1
p2
0.25
0.2
0.15
Inductive
shunting
0.1
Resistive
shunting
0.05
0
0.1
0.2
0.5
1
2
Frequency ratio
5
10
!0i=!i
Figure 4.7: Evolution of the damping ratio of the inductive and resistive shunting
with the de-tuning of the structural mode. ωi is the natural frequency for which
the shunt has been optimized, ωi0 is the actual value (k = 0.5, νi = 0.3).
4.3.6
Summary (1): maximum attainable damping
The maximum attainable damping ratios with the three different shunts (R and
series and parallel RL) are given by Eqs. 4.26, 4.37 and 4.43, respectively; these
equations are formulated in terms of Ωi and ωi (open-circuit and short-circuit
natural frequencies) and are summarized in Table 4.1. These results are exact as
long as the modal density around the ith mode is low. Table 4.1 also presents
approximate formulae in terms of k 2 and νi ; they are based on Eq. 4.15 and on
the assumption that Ωi ≈ ωi ; they highlight the influence of k 2 and νi on the
shunt performances. In all cases the damping performances are controlled by the
generalized coupling factor Ki .
60
shunt
ξimax (exact)
ξimax (approximate)
R
Ωi − ωi
K2
≈ i
2ωi
4
k 2 νi
4(1 − k 2 )
s
series RL
1
2
parallel RL
1
2
s
Ω2i − ωi2
Ki
≈
2
2
ωi
1
2
Ω2i − ωi2
Ki
=
2
2
Ωi
1
2
r
r
k 2 νi
1 − k2
k 2 νi
1 − k2
Table 4.1: Attainable damping ratios with various passive shunts. The approximate formulae are based on Eq. 4.15 and on the assumption that Ωi ≈ ωi . Ki is
the generalized electromechanical coupling factor (Eq. 4.13).
4.3.7
Summary (2): optimal values of the components
The optimal values of the electrical components (i.e., those for which the structural damping ξi is maximal) are given, for the different shunts, by Eqs. 4.27,
4.35 and 4.42, respectively; these formulae are summarized in the left part of
Table 4.2. Note that:
1. In most cases one has ωi /Ωi ≈ 1.
2. The Ck 2 νj factors defining Ci2 (Eq. 4.19) are generally very small; for the
first few modes, Ci2 can thus be approximated by:


n
X
Ci2 ≈ C 1 − k 2 + k 2
νj  = Cstatic
(4.44)
j=1
where Cstatic (defined in Eq. 4.11 and Eq. 4.12) is the capacitance of the
structure measured under static conditions.
As a consequence, Eq. 4.27, 4.35 and 4.42 can be approximated as indicated in the
right part of Table 4.2. These approximate formulae have been used throughout
this work to tune the different shunts, with or without negative capacitance. In
the case of RL shunts, however, a little trial and error was necessary to account
for the imprecisions of the gyrator circuits.
4.4
Application to the truss
This section applies the analytical formulae developed in §4.3 to the benchmark
truss structure. Two kinds of parameters are analyzed: (i) the maximum attainable damping ratio ξi and (ii) the optimal value of the electrical components.
4.4 Application to the truss
shunt
Lopt
R
n.a.
series RL
parallel RL
61
exact
Ropt
r
ωi2
Ci2 Ω4i
ωi 1
Ωi Ωi C2
s
2ωi
Ω2i − ωi2
Ci2 Ω2i
Ω2i
1
Ci2 ωi2
1
p
2 Ω2i − ωi2 Ci2
Lopt
approximate
Ropt
n.a.
1
ωi Cstatic
ωi2
1
Cstatic
2Ki
ωi Cstatic
1
Cstatic
1
ωi2
2 ωi Cstatic Ki
Table 4.2: Optimal values for R (in Ohm) and L (in Henry). Ci2 is defined in
Fig. 4.4b and Eq. 4.19, and Cstatic in Eq. 4.11 and Eq. 4.12. The approximate
formulae are based on the fact that Ωi ≈ ωi and that, for the first few modes,
Ci2 ≈ Cstatic .
Because the series and parallel RL shunts have very similar performances, only
the series shunt is further investigated. Experimental results are presented in
chapter 5.
Maximum attainable damping
Three different methods can be used to predict the performances, from the easiest
to the most involved:
• (1) One can use the computed ωi and νi (Table 2.3), the transducer coupling factor k 2 and the assumption that the shunt does not change the
structural mode shapes. Ωi and Ki are in this case predicted with the approximate equations 4.15 and 4.16, and the maximum attainable damping
ξi is predicted with the approximate formulae in Table 4.1.
• (2) The Ωi can also be directly computed with the specific FE model (SAMCEF), by changing the electrical boundary conditions (open-circuit). The
maximum damping ratio ξi is then estimated with the “exact” formulae
in Table 4.1, which are based on the less restrictive assumption of well
separated modes and do not use the νi and k 2 parameters.
• (3) Finally, the maximum structural damping ratios ξi can be directly
evaluated by means of the full MATLAB model, which couples the FE
model and the electrical network. The comparison with (2) gives an idea
of the influence of the modal coupling.
62
ωi /2π
mode
1
2
18.92
22.52
Ωi /2π
(1)
(2)
Eq. 4.15 FE model
19.07
19.02
23.53
22.53
Ki (%)
(1)
(2)
Eq. 4.16 FE model
12.88
10.39
3.00
2.45
Table 4.3: Predicted Ωi (in Hz ) and Ki (in %); (1) approximate formulae based
on νi and k 2 , (2) FE model.
mode
1
2
max (%)
ξR
(1)
(2)
(3)
0.42
0.27
0.27
0.022 0.015 0.015
max (%)
ξRL
(1) (2) (3)
6.50 5.19 5.20
1.50 1.22 1.17
Table 4.4: Predicted maximum modal damping ξi (in %) for the R and series RL
shunts. (1) Approximate formulae in Table 4.1 based on νi and k 2 , (2) “exact”
formulae in Table 4.1 based on the computed ωi and Ωi , (3) full MATLAB model.
Table 4.3 compares the values of Ωi and Ki obtained with methods (1) and
(2). The results are comparable, even though the approximate formulae slightly
overestimate Ki . The approximate formulae based on k 2 and νi are much more
precise in this case than in the case of the IFF (chapter 3), because shunt damping
has much less influence on the mode shapes than the force feedback.
Next, Table 4.4 compares the maximum attainable damping ξi obtained, for
the R and series RL shunts, with the three different methods. The approximate formulae slightly overestimate the maximum attainable damping too; on
the other hand, the influence of the modal coupling is negligible. The shunt performances can thus be accurately predicted from the knowledge of the Ωi and ωi
(method (2)) only.
Choice of the components
Table 4.5 compares, for the first two modes, the optimum values of R and L given
by the ‘exact’ and ‘approximate’ formulae in Table 4.2 with those obtained from
the fully coupled MATLAB model. The ‘exact’ formulae are based only on the
assumption of well separated modes while the ‘approximate’ formulae also rely
on the assumption that ωi /Ωi ≈ 1 and that Ci2 ≈ Cstatic . The consistency of the
various formulae was found to be quite good.
4.5 References
mode
1
2
Ropt (R shunt)
(1)
(2)
(3)
68794 68981 68981
57772 58376 59894
63
Ropt (RL shunt)
(1)
(2)
(3)
14370 14371 14263
2829
2859
3062
Lopt (RL shunt)
(1)
(2)
(3)
578.9 572.7 571.8
408.3 412.5 423.3
Table 4.5: Predicted optimal values of the components (in Ω and H) for the
R and series RL shunts. (1) approximate formulae in Table 4.2, (2) “exact”
formulae in Table 4.2, (3) full MATLAB model.
4.5
References
S. Alessandroni, U. Andreaus, F. dell’Isola, and M. Porfiri. A passive electric
controller for multimodal vibrations of thin plates. Computers and Structures,
83:1236–1250, 2005.
A. Antoniou. Realisation of gyrators using operational amplifiers, and their use
in RC-active-network synthesis. Proc. IEE., 116(11):1838–1850, Nov. 1969.
P. Bisegna, G. Caruso, and F. Maceri. Optimized electric networks for vibration
damping of piezoactuated beams. Journal of Sound and Vibration, 289:908–
937, 2006.
G. Caruso. A critical analysis of electric shunt circuits employed in piezoelectric
passive vibration damping. Smart Materials and Structures, 10:1059–1068,
2001.
W.W. Clark. Vibration control with state-switched piezoelectric materials. Journal of Intelligent Material Systems and Structures, 11:263–271, April 2000.
C.L. Davis and G.A. Lesieutre. A modal strain energy approach to the prediction
of resistively shunted piezoceramic damping. Journal of Sound and Vibration,
184(1):129–139, 1995.
D.L. Edberg, A.S. Bicos, C.M. Fuller, J.J. Tracy, and J.S. Fechter. Theoretical
and experimental studies of a truss incorporationg active members. J. of Intell.
Mater. Syst. and Struct., 3:333–347, April 1992.
R.H. Edwards and R.H. Miyakawa. Large structure damping tasks report. Technical Report 4132.22/1408, Hughes Aircraft Co., 1980.
Optics, 18(5):690–697, March 1979.
64
References
D. Guyomar and C. Richard. Non-linear and hysteretic processing of piezoelement: Application to vibration control, wave control and energy harvesting.
International Journal of Applied Electromagnetics and Mechanics, 21:193–207,
2005.
M.H. Holnusen and K.A. Cunefare. Damping effects on the state-switched absorber used for vibration suppression. Journal of Intelligent Material Systems
and Structures, 14:551–561, Sept. 2003.
G.A. Lesieutre, G.K. Ottman, and H.F. Hofmann. Damping as a result of piezoelectric energy harvesting. Journal of Sound and Vibration, 269:991–1001,
2004.
C. Maurini. Piezoelectric Composites for Distributed Passive Electric Control:
Beam Modelling, Modal Analysis, and Experimental Implementation. PhD
thesis, Université Pierre et Marie Curie (Paris) and Università di Roma “La
Sapienza”, 2005.
C. Maurini, F. dell’Isola, and D. Del Vescovo. Comparison of piezoelectronic
networks acting as distributed vibration absorbers. Mechanical Systems and
Signal Processing, 18:12431271, 2004.
D. Niederberger. Smart Damping Materials Using Shunt Control. PhD thesis,
Swiss federal institute of technology (ETH) Zurich, 2005.
D. Niederberger, A. Fleming, S.O.R. Moheimani, and M. Morari. Adaptive multimode resonant piezoelectric shunt damping. Smart Materials and Structures,
13:1025–1035, 2004.
C.H. Park and D.J. Inman. Enhanced piezoelectric shunt design. Shock and
Vibration, 10:127–133, 2003.
M. Porfiri. Performances of Passive Electric Networks and Piezoelectric Transducers for Beam Vibration Control. PhD thesis, Università di Roma “La
Sapienza” and Université de Toulon et du Var, 2005.
References
65
2002. 2nd edition.
K.H. Rew and I. Lee. Adaptive shunting for vibration control of frequencyvarying structures. Journal of Guidance, Control and Dynamics, 24(6):1223–
1224, Nov.-Dec. 2001.
J. Tang and K.W. Wang. Active-passive hybrid piezoelectric networks for vibration control: Comparisons and improvement. Smart Materials and Structures,
10:794–806, 2001.
S.Y. Wu. Method for multiple mode piezoelectric shunting with single PZT
transducer for vibration control. Journal of Intelligent Material Systems and
Structures, 9:991–998, Dec. 1998.
H. Yu and K.W. Wang. Piezoelectric networks for vibration suppression of mistuned baled disks. ASME Journal of Vibration and Accoustics, 129:559–566,
Oct 2007.
66
References
Chapter 5
Active shunt damping with a
negative capacitance
5.1
Introduction
The importance of the electromechanical coupling factor k 2 in the shunt damping
performances of piezoelectric structures was stressed in chapter 4. This k 2 factor
depends on the material and on the actuation mode; for PZT piezoceramics,
one typically has k 2 ≈ 0.5, and some new materials such as PMN-PT are even
reported with a k 2 as high as 0.8 or 0.9.
According to Eq. 2.17, the value of k 2 is limited by the intrinsic electrical capacitance of the piezoelectric transducer. As early as 1979, Forward proposed
the use of an active electronic circuit that would artificially decrease the capacitance of the transducer and thus increase the conversion of mechanical energy
into electrical energy: the so-called ‘negative capacitance’ shunt (Fig. 5.1). This
‘negative capacitance’ does not by itself dissipate energy, but it does enhance the
dissipation of energy in the passive electric circuit Z. Although Forward took a
patent for his invention, he did not publish any experimental results. The concept
then remained largely forgotten for 20 years, until some researchers re-introduced
the idea (Wu, 2000; Date et al., 2000; Tang and Wang, 2001). Since then, the
concept has been used in various experimental set-ups (e.g. Behrens et al., 2003;
Park and Baz, 2005; Kim et al., 2005; Bisegna et al., 2006; Neubauer et al., 2006;
Yu et al., 2006).
The negative capacitance is an active circuit that can destabilize the structure
if improperly tuned. In Forward’s patent, the negative capacitance circuit is
placed in parallel to the electrodes of the transducer (Fig. 5.1a). Although some
authors follow this implementation (Wu, 2000; Park and Baz, 2005), most of
67
68
Z
-C’
Z
(a)
-C’
(b)
Figure 5.1: Principle of the negative capacitance shunt. a) Parallel shunt; b)
series shunt. Z is a passive electrical circuit used to dissipate energy, and −C 0 is
an active circuit simulating the behavior of a negative capacitance.
them prefer another implementation where the negative capacitance circuit is
connected in series with the transducer (Fig 5.1b). In this chapter we show that,
although both implementations enhance the electromechanical coupling of the
structure, their behavior and stability limits are widely different, and that the
series implementation is more robust than the parallel one. This may explain the
absence of experimental results by Forward. More specifically, our contribution
can be summarized as follows:
1. We show that, in both implementations, the shunted transducer can be
seen as an equivalent transducer with different characteristics and enhanced
electromechanical coupling coefficient.
2. A simple method for the prediction of the performances and the stability analysis is introduced; it is based on the electrical admittance of the
actuator.
3. We propose a new electrical circuit that enhances the robustness of the
parallel shunt.
5.2
Effects on a transducer
This section analyzes the effects of the shunt on the transducer alone; the next
section considers the situation where the transducer is embedded into a mechanical structure.
5.2.1
Parallel negative capacitance
Consider a general piezoelectric linear actuator. Its constitutive equations were
described in chapter 2 (Eq. 2.16):
5.2 Effects on a transducer
Qt
69
Q
Qt
Qs
V
-C´
k ã2 =
k 2C
CàC 0
V
Cã = C à C0
a) Piezo
b) Equivalent piezo
(C ?; k ?2)
Figure 5.2: a) Piezoelectric transducer connected in parallel to a negative capacitance −C 0 ; b) equivalent transducer.
½ ¾ ·
¸½ ¾
Q
C
nd33
V
=
∆
nd33 1/Ka
f
(5.1)
With C the constant-force capacitance of the stack, Ka its short-circuit stiffness,
n the number of discs in the stack and d33 a coupling constant of the piezoelectric
material. If the transducer is connected in parallel to a negative capacitance of
value −C 0 , as in Fig. 5.2a, it is readily found that the shunted system is equivalent
to a “simple” transducer with the same n, d33 and Ka parameters and a lower
capacitance, as shown in Fig. 5.2b. Indeed, the total electrical charge Qt flowing
in the system is given by:
C0
Qt = Q −
(5.2)
V
and, from Eq. 5.1 and Eq. 5.2, the characteristic equations of the shunted transducer are:
½ ¾ ·
¸½ ¾
Qt
C − C 0 nd33
V
=
(5.3)
∆
nd33
1/Ka
f
which is identical to Eq. 5.1, but with a lower capacitance (C − C 0 ) instead of C.
Besides, from Eq. 2.17 defining k 2 , the equivalent piezoelectric coupling factor
k ∗2 is given by:
k2 C
(5.4)
k ∗2 =
C − C0
Thus, the negative capacitance shunting can be seen as a way of improving the
conversion of energy in the transducer. The shunt also increases the open-circuit
stiffness Ka /(1 − k ∗2 ) of the transducer and therefore the open-circuit natural
frequencies of the structure Ωi .
70
Q -C’
Vt
V
Q
k *2 =
Vt
k 2C '
C' -CS
a) Piezo
b) Equivalent piezo
(C ?; k ?2; d ?33; K ?a)
Figure 5.3: Piezoelectric transducer connected in series to a negative capacitance
−C 0 and equivalent transducer.
Note, finally, that if C 0 > C S = C(1 − k 2 ), one has k ∗2 > 1 and the equivalent
transducer is no longer passive.
5.2.2
Series negative capacitance
If the transducer is connected in series to a negative capacitance of value −C 0 ,
as shown in Fig. 5.3a, one immediately finds:
and, with Eq. 5.1:
Vt = V − Q/C 0
(5.5)
½ ¾ · ∗
¸½ ¾
Q
C
nd∗33
Vt
=
∆
nd∗33 1/Ka∗
f
(5.6)
where we have defined:
Ka∗ =
Ka (C 0 − C)
C0 − CS
C∗ =
C
1 − C/C 0
d∗33 =
d33 C 0
C0 − C
(5.7)
with C S = C(1−k 2 ) the constant-volume capacitance of the transducer. Besides,
the piezoelectric coupling factor becomes:
k ∗2 =
k2 C 0
C0 − CS
(5.8)
If C 0 > C, the new system is totally equivalent to a “simple” piezoelectric transducer with smaller stiffness Ka∗ and higher capacitance C ∗ , d∗33 coefficient and
electromechanical coupling factor k ∗2 . The open-circuit stiffness, on the other
hand, does not change: Ka∗ /(1 − k ∗2 ) = Ka /(1 − k 2 ).
5.3 Shunt-structure interaction and stability
71
The effects of a series negative capacitance are thus opposite to those of the
parallel shunt: the short-circuit natural frequencies ωi decrease and the opencircuit natural frequencies Ωi are not affected. The result is however the same:
the ratio Ωi /ωi increases, which, from Table 4.1, leads to improved performances
of the R and RL shunts.
Note that, for C S < C 0 < C, k ∗2 is greater than one and Ka∗ is negative: the
transducer is no longer passive. Stability limits are investigated in more detail in
the next section.
5.3
Shunt-structure interaction and stability
Shunt damping of piezoelectric structures can be regarded as a control system
where the piezoelectric element plays the role of both actuator and sensor and,
as such, should benefit from the guaranteed stability of collocated systems (see
chapter 1). However, when implementing the parallel negative capacitance as
proposed by Forward (1979) or Park and Baz (2005), high-frequency modes became destabilized. This motivated a more complete stability assessment, which
is presented in this section.
To this end, the re-writing of the shunt-structure interaction in the form of the
feedback diagrams of Fig. 5.4a and Fig. 5.4b was useful. Zstructure (Ystructure ) is
the electrical impedance (admittance) of the piezoelectric structure, and Yshunt
(Zshunt ) is the admittance (impedance) of the shunt circuit; each can be obtained
either from numerical simulations or from experimental measurements. This
feedback scheme has been used in Matlab to produce all the numerical results
presented in this work; it can handle many kinds of electrical circuits and it can
easily be generalized to structures with several piezos and multi-port electrical
circuits.
5.3.1
Parallel shunt
It was shown in chapter 4, §4.2.2, that the open-circuit poles of a piezoelectric
structure are given by the zeros of its electrical admittance Ystruct (s). The result
is in fact more general: the theory of electrical networks (e.g. Deliyannis et al.,
1999) states that the open-circuit poles of any two-terminal electrical network
are given by the zeros of its admittance.
In particular, when an electric circuit with admittance Yshunt is connected in
parallel to a piezoelectric structure, as shown in Fig. 5.4a, the open-circuit poles
of the new system (i.e., those for which I = 0) are the zeros of the equivalent
72
Ip
I
I
Is
V
+
Ip
Z structure
V
à
Y
Is
Yshunt
Ytot
(a)
I
V
V
Z
Vs
+
Vs
Vp
Vp
à
Ystructure
I
Zshunt
Z tot
(b)
Figure 5.4: a) parallel shunt of a piezoelectric structure and its feedback representation; b) series shunt.
Q
V
S
2
C =C(1-k )
Cstatic
0
Hz
a)
b)
Figure 5.5: a) Capacitance Q/V of a piezoelectric transducer embedded in a
fictitious 3-mode structure. b) Evolution of the open-circuit natural poles Ω∗i
when C 0 increases (parallel shunt).
73
admittance Ytot , with Ytot classically given by:
Ytot (s) = Ystruct (s) + Yshunt (s)
(5.9)
The foregoing result can also be demonstrated with the feedback diagram in
Fig. 5.4a: indeed, according to this diagram, the new open-circuit poles are given
by:
1 + Zstruct (s) Yshunt (s) = 0
(5.10)
or, if the poles of Zstruct and the zeros of Yshunt are distinct:
Ystruct (s) + Yshunt (s) = Ytot (s) = 0
(5.11)
In this work the new open-circuit natural frequencies are denoted Ω∗i ; of course,
if Yshunt → 0, on has Ω∗i → Ωi .
Let us apply this result on a structure shunted by a negative capacitance, i.e.
Yshunt = −sC 0 . The structural admittance Ystruct (s) is given by Eq. 4.8: it is
shown (multiplied by 1/s) in Fig. 5.5a for a fictitious, undamped, three-mode
structure. When the shunt −sC 0 is connected, the total admittance Ytot is given
by the same curve, but translated vertically by −C 0 . The new open-circuit natural
frequencies Ω∗i are at the intersection of the new curve with the X-axis; the shortcircuit ones ωi∗ , by contrast, are not affected by a parallel shunt (ωi∗ = ωi ).
Fig. 5.5b shows (in the complex plane) the evolution of the open-circuit poles as
C 0 increases.
• If C 0 < C S = C(1 − k 2 ), they migrate on the imaginary axis, with Ω∗i > Ωi :
the system remains stable, and the ratios Ω∗i /ωi∗ increase, which is consistent
with the results of §5.2.1.
• For C S < C 0 < Cstatic , the last pair (±jΩ∗3 in this case) disappears at
infinity and reappears symmetrically at infinity on the real axis, moving
towards the origin; because of the presence of a pole on the Right Half
Plane, the system is not open-circuit stable.
• If C 0 > Cstatic , the last pair reintegrates the imaginary axis (below ω1 ). The
system is thus open-circuit stable, but it is not passive, because the lowfrequency admittance is negative and because it starts with a zero instead
of a pole. Connecting such a system to an electrical network (even passive,
such as R or RL circuits) may destabilize it.
The foregoing analysis is especially useful because, with a single admittance curve,
one can determine the position of the open-circuit natural frequencies Ω∗i for a
74
-1
1.5
0
-1
1
First mode
-2
First mode
0.5
-3
-1
a)
-0.5
0
b)
Figure 5.6: Nyquist plots of the truss structure shunted with: a) a parallel negative capacitance, and b) a series negative capacitance. Both shunts were tuned
at approximately 90% of the stability limit and a resistor R was also introduced
in the circuit.
given value of the negative capacitance C 0 , and thus the performances of the R or
RL shunt (with the formulae of Table 4.1). It also makes apparent some major
drawbacks of the method:
1. The instability comes from high-frequency dynamics of the structure, which
are difficult to model.
2. Even when C 0 is close to the stability limit, the first frequencies Ω∗1 and Ω∗2
do not increase by much: this is due to the very stiff slopes of the Q/V curve
(Fig. 5.5a). The effects of the parallel shunt are thus more pronounced for
high-frequency modes.
To analyse further the stability of the shunt, a Nyquist plot of the open-loop
transfer function (in the sense of Fig. 5.4a, i.e. Zstruct (s)Yshunt (s)) is presented in
Fig. 5.6a. Zstruct was measured1 on the truss structure as explained in section 5.4,
and Yshunt was modelled in Matlab. A resistor R tuned to damp the first mode
of the truss was also introduced in the system. It appears that the first mode
is reasonably distant from the (−1, 0) point; higher-frequency modes however,
although theoretically stable, are extremely close to instability. As a consequence,
non-modelled behavior of the structure (such as piezoelectric non-linearities or
the finite bandwidth of the shunt) could make them unstable. In practice, once
the shunt was implemented and connected, instabilities occurred for values of C 0
as low as 50% of the theoretical stability limit.
1
between 2.36 Hz and 100 kHz
Rp
à R neg
75
-1
0
-1
à C0
R
-2
First mode
-3
a)
b)
Figure 5.7: a) Proposed modifications for the parallel shunt (compare with
Fig. 5.4); b) Nyquist plot of the modified system (compare with Fig. 5.6a).
To overcome this, the shunt was modified according to Fig. 5.7a. This configuration was chosen after some trial-and-errors: it introduces some roll-off in the
FRF of Yshunt (s) and has thus a positive influence on the stability. The Nyquist
plot of the modified system, with the shunt once again at 90% of the stability
limit, is presented in Fig. 5.7b; this time most of the curve is reasonably far away
from the (−1, 0) point.
The stability of the modified system is not guaranteed: it must thus be assessed
on a case-by-case basis, by means of Nyquist plots and measured Zstruct curves,
which can be quite difficult to obtain. A necessary (but not sufficient) stability
condition for the modified system is:
Rneg > Rp
(5.12)
The use of the modified system was found to be more difficult than that of the
series negative capacitance shunt, which is presented in the next section.
5.3.2
Series shunt
The methodology follows closely that of the previous section. Consider a piezoelectric structure connected in series to a general electric circuit with impedance
Zshunt , as described in Fig. 5.4b. With the feedback diagram of Fig. 5.4b, it is
found that the new short-circuit poles (those with V = 0) are given by:
Ztot (s) = Zstruct (s) + Zshunt (s) = 0
(5.13)
76
V
Q
1
C(1-k2 )
1
Cstatic
0
Hz
Figure 5.8: Impedance sZ = V /Q of a fictitious, undamped, three-mode structure
where Ztot is the equivalent impedance of the new system as described in Fig. 5.4b.
Thus, when the shunt is connected in series, the short-circuit poles of the new
system are given by the zeros of the equivalent impedance Ztot (s).
Zstruct is merely the inverse of Eq. 4.8: it is shown (multiplied by s) in Fig. 5.8.
If Zshunt = −1/sC 0 , the behavior of the shunted system is thus governed by the
curve in Fig. 5.8 translated vertically by −1/C 0 , and the new short-circuit natural
frequencies ωi∗ are given by the intersection of this curve with the X-axis. The
open-circuit frequencies Ω∗i are not affected by a series shunt. Once again, the
knowledge of a single impedance curve allows the prediction of the performances
of a R or RL shunt (from the formulae of Table 4.1) for a given value of the
negative capacitance −C 0 .
The short-circuit natural frequencies ωi∗ decrease when C 0 increases, which is
consistent with the results of §5.2.2. The acceptable values for the shunt are
those which verify2 C 0 > Cstatic . Note that C 0 = Cstatic is also the limit for which
the (now negative) stiffness of the transducer exactly cancels K ∗ , the stiffness
of the structure seen from the end points of the transducer. A Nyquist plot of
the open-loop transfer function Ystruct (s)Zshunt (s) is shown in Fig. 5.6b; a resistor
R has been introduced in the circuit so as to optimally damp the first mode. It
appears that the high-frequency modes are far enough from the (−1, 0) point: the
shunt does not need to be modified. The situation is thus much more favorable
2
Cstatic , defined in Eq. 4.11 and Eq. 4.12, is the capacitance of the structure measured under
static conditions.
77
than in the parallel case, as:
• The stability limit concerns low-frequency modes of the system, which are
easier to measure or model (it is unavoidable that a part of the curve be close
to the (−1, 0) point; the closer to this point, the higher the performances).
• This time, ω1∗ decreases by much more as C 0 approaches the stability limit
(it goes down to the origin, at least theoretically). This strategy tends to
be more effective for low-frequency modes.
• The capacitance C ∗ of the equivalent transducer increases (in contrast to the
parallel case), which reduces the optimal value Lopt of the inductor in a RL
shunt (see Table 4.2) and thus makes it easier to implement electronically.
5.3.3
Sensitivity
øR
1
0.08
0.06
Unstable
0.04
0.02
0
1
1.2
1.4
0
1.6
1.8
C =C static
Figure 5.9: Theoretical evolution of the maximum attainable damping for the
first mode of the truss when the negative capacitance changes (R shunt + series
negative capacitance).
“Good” performances generally require that the active shunt be tuned close to
the stability limit, which is a major drawback. This issue is illustrated in Fig. 5.9,
which displays the theoretical evolution of the maximum attainable damping for
the first mode of the truss when a series negative capacitance is introduced (R
78
shunt). The added damping ξ1R drops from 3% to 1.5% when the ratio C 0 /Cstatic
changes from 1.1 to 1.2, and to 0.53% when C 0 /Cstatic = 2 (ξ1R = 0.27% without
negative capacitance). As explained in §5.3.2, the system becomes unstable when
C 0 /Cstatic < 1.
5.3.4
Nonlinearity
To conclude this section, let us point out that the capacitance of a piezo transducer is variable with respect to the excitation level and that it depends much
on the ambiant temperature. In most applications this has no importance, but
here the performances and stability rely on a fine tuning of the negative capacitance with respect to the capacitance of the piezo. A sudden change of C can
decrease substantially the performances of the shunt or, worse, make it unstable.
The designer must therefore be cautious and take reasonable stability margins.
Throughout this work and for the purpose of illustration the negative capacitances
were tuned as close as 90% of the stability limit; this was made possible by an
accurate knowledge of the structural impedance. In realistic situations where
the uncertainties on the impedance curve are much larger, negative circuits at
60-70% of the limit would be more advisable.
5.4
5.4.1
Implementation of the negative capacitance
1
Z0 = à R
R2 Z
I
Z
V
Op Amp
R1
R2
Figure 5.10: Parallel negative impedance. The series one is identical but with
the + and − pins inverted (Philbrick Researches Inc., 1965).
The negative capacitance shunts, both parallel and series, were implemented as
described in Fig. 5.10 (Philbrick Researches Inc., 1965); it is a simple circuit
79
involving an operational amplifier (OPA445 in this case).
In this work the best results were obtained when the impedance Z consisted in
another piezoelectric stack with the same capacitance as that of strut 1; although
not essential (it could have been replaced by a “common” capacitance), it allows
us to decrease the effects of the actuator’s non-linearities mentioned in §5.3.4.
We took R1 = 11kΩ and R2 = 10kΩ in the parallel case, and the opposite
in the series case; the circuits were thus approximately at 90% of the stability
limit. In the parallel case, Rp and Rneg were chosen to be 15kΩ and 16.5kΩ,
respectively. No instability was ever observed with this circuit and the optimal
R or RL components.
5.4.2
Impedance measurement
Impedance meters with a measurement range starting from DC and a sufficient
frequency resolution are very difficult to find. The impedance of the structure,
seen from the electrodes of strut 1, has been measured with an Agilent 4294A
impedance analyzer between 40 Hz and 100 kHz. At lower frequency we measured
separately the current flowing into the piezo and the voltage across it, and we
calculated the transfer function V /I with a Fourier analyzer HP 35670A; numerous calibration processes were run to ensure the correctness of the measurements.
The result |Q1 /V1 | (in Coulomb/V olt) is shown in Fig. 5.11.
-7
3
x 10
jQ =V j
2
1
0
0
10
1
10
2
10
3
10
4
10
5
10
Hz
Figure 5.11: Experimental admittance |Q1 /V1 | of the truss (in Cb/V ).
This impedance curve has already been used to present the Nyquist plots in
Fig. 5.6a-b and Fig. 5.7b. Besides, Fig. 5.12a shows the equivalent impedance of
the structure with a parallel and series negative capacitance (Fig. 5.12b shows the
corresponding numerical results). These measurements confirm that the series
shunt decreases the short-circuit natural frequencies ωi∗ , that the parallel shunt
80
|Z| (dB)
|Z| (dB)
b)
a)
130
130
Òã1
120
Parallel shunt
110
110
Ò1
100
100
No shunt
!1
90
90
80
Series shunt
80
70
70
60
120
! ã1
10
20
Hz
30
40
50
60
10
20
Hz
30
40
50
Figure 5.12: Equivalent impedance with and without the negative capacitive
shunt. a) Experimental; b) simulations.
increases the open-circuit frequencies Ω∗i , and that both shunts increase the ratio
Ω∗i /ωi∗ ; this is especially apparent for mode 2 (22 Hz), which barely appears
in the open-loop curve, but is much more visible once a negative capacitance
is connected to the piezo. The generalized electromechanical coupling factor of
mode 1, K1 3 , increased from 10.5% to approximately 30.5%, and K2 , which could
not be measured without the negative capacitance, reached approximately 14%
when the active shunts were connected.
5.4.3
R shunts
The FRF between the voltage at strut 2 and the force in strut 1 has been measured
with a HP 35670A Fourier analyzer. It is shown in Fig. 5.13, first when the shunt
is purely resistive (R = 62kΩ), then when a series or parallel negative capacitance
has been added (R = 6kΩ and 510kΩ, respectively). The R shunt alone can
increase the damping of mode 1 from 0.18% to 0.43%. The negative capacitance
shunts can increase it to approximately 3%.
The locus of the first pole of the structure was also recorded as R varied from
0 → ∞. It is shown in Fig. 5.14. Two measurements were made for each value of
R; each time the poles were automatically identified by the Fourier analyzer. The
solid line represents theoretical predictions based on Eq. 4.25 and the identified
poles and zeros ω1 and Ω1 ; the agreement between theory and experiment is very
s
3
defined by K1 =
Ω21 − ω12
, see §4.2.3.
Ω21
20
R + parallel
negative
capacitance
Open-circuit
R only
10
Amplitude (dB)
81
R + series
negative
capacitance
0
-10
-20
-30
-40
14
16
18
20
22
24
26
28
Freq. (Hz)
Figure 5.13: Response of the structure with different resistive shunts.
ø = 0:43%
ø = 2:9%
19
18.5
Resistive shunt
+ series negative
capacitance
-0.5
-0.4
Im (Hz)
Resistive shunt
only
18
-0.3
Real (Hz)
-0.2
-0.1
Figure 5.14: Root locus of the system shunted with a resistor and a series negative
capacitance. The dots represent experimental measurements; two measurements
were performed for each value of R. The solid lines were traced according to
Eq. 4.25 and the identified ωi and Ωi . Different scales are used for the X and Y
axis.
82
References
good.
Finally, a second locus was measured with a series negative capacitance shunt and
a resistor; it is also shown in Fig. 5.14. It merely confirms the conclusions of §5.4.2:
a series negative capacitance decreases the short-circuit natural frequencies ωi∗ ,
has no impact on the open-circuit natural frequencies Ω∗i , and widens the loop
of the locus. The dashed line indicates a part of the locus which, due to the
smallness of the resistor R, has very small stability margins and thus could not
be measured.
5.4.4
RL shunts
A synthetic inductance L was implemented with the electronic circuits described
in Fig. 4.2 (gyrators). Its value and that of the series resistance were tuned so as
to minimize the amplitude of the FRF from piezo 2 to force sensor 1 (final values:
L ≈ 570H, R = 6kΩ). The result is shown in Fig. 5.15a , and the corresponding
simulation results (with the best fit L = 576H) are shown in Fig. 5.15b). The
damping ratios of the two pairs of poles was identified to be 2.7% and 2.5%,
respectively. It is worth noticing that a passive RL shunt alone performs as well
as an active “negative capacitance + R” shunt. For the purpose of comparison,
the performances of the IFF (with a gain such that the first mode is critically
damped) are also shown in the figure.
The FRF when piezo 1 is shunted by a series negative capacitance and an optimum RL circuit is also shown in Fig. 5.15a (L ≈ 54H, R = 2kΩ), and the
simulation results (with the best fit L = 57.5H) is also shown in Fig. 5.15b. The
damping ratios of the two pairs of poles are 9.3% and 5.4%, respectively. Quite
remarkable is the behavior of the second mode (at 22 Hz): while the passive
shunts have hardly any influence on it (because of its weak controllability from
strut 1), the RL shunt with a negative capacitance can raise its damping ratio
from 0.18% to 1.0%.
Finally, the three different root loci (the resistive shunt with and without negative
capacitance and the one for the IFF) are gathered on a single graph in Fig. 5.16.
The vicinity of ωi had to be enlarged because the loci with shunt damping are
much smaller than the locus of the IFF. The different natural frequencies (z1 , ω1 ,
ω1∗ and Ω1 ) can be seen.
5.5
References
S. Behrens, A.J. Fleming, and S.O.R. Moheimani. A broadband controller for
shunt piezoelectric damping of structural vibration. Smart Materials and Struc-
References
83
20
a)
10
Open-circuit
Amplitude (dB)
0
RL only
-10
RL + negative
capacitance
-20
-30
-40
Integral Force
Feedback
-50
-60
5
10
15
20
25
30
35
40
35
40
Freq. (Hz)
20
10
b)
Amplitude (dB)
0
-10
-20
-30
-40
-50
-60
5
10
15
20
25
30
Freq. (Hz)
Figure 5.15: a) FRF of the structure with RL shunts and IFF active control; b)
corresponding simulation results.
84
References
20
IFF
15
R shunt
10
5
z1
-20
-15
-10
-5
Im (Hz)
Ò1
IFF
Negative
capacitance
!1
ã
!1
0
Real (Hz)
Figure 5.16: Identified root locus of the IFF; the root loci of the R shunts are also
represented for the purpose of comparison. The vicinity of ω1 has been enlarged.
tures, 12:18–28, 2003.
937, 2006.
M. Date, M. Kutani, and S. Sakai. Electrically controlled elasticity utilizing
piezoelectric coupling. J. Applied Physics, 87(2):863–868, Jan. 2000.
T. Deliyannis, Y. Sun, and J.K. Fidler. Continuous-Time Active Filter Design.
CRC Press, 1999.
R.L. Forward. Electromechanical transducer-coupled mechanical structure with
negative capacitance compensation circuit. Us patent 4,158,787, 1979.
J.S. Kim, K.W. Wang, and E.C. Smith. High-authority piezoelectric actuation
system synthesis through mechanical resonance and electrical tailoring. J. of
Intelligent Material Systems and Structures, 16:21–31, Jan. 2005.
M. Neubauer, R. Oleskiewicz, K. Popp, and T. Krzyzynski. Optimization of
damping and absorbing performance of shunted piezo elements utilizing negative capacitance. Journal of Sound and Vibration, 298:84–107, 2006.
References
85
C.H. Park and A. Baz. Vibration control of beams with negative capacitive
shunting of interdigitated electrode piezoceramics. Journal of Vibration and
Control, 11:331–346, 2005.
Philbrick Researches Inc. Application manual for computing amplifiers for modelling, measuring, manipulating & much else. Technical report, Nimrod Press,
Boston, 1965.
10:794–806, 2001.
S.Y. Wu. Broadband piezoelectric shunts for structural vibration control. Us
patent 6,075,309, 2000.
H. Yu, K.W. Wang, and J. Zhang. Piezoelectric networking with enhanced
electromechanical coupling for vibration delocalization of mistuned periodic
structures-theory and experiment. Journal of Sound and Vibration, 295:246–
265, 2006.
86
References
Chapter 6
Single-axis isolation
6.1
Introduction
Active vibration isolation has been studied at the Active Structures Laboratory
(ULB) since 2000, in the context of space applications. Emphasis has been placed
on robustness, which has led to the use of decentralized, collocated control with
Integral Force Feedback (IFF). Two multi-axis isolators were successively built
and tested in a micro-g environment; they were shown to effectively attenuate the
vibration propagation (Abu Hanieh, 2003; Preumont et al., 2007). These prototypes employed electromagnetic (moving-coil) actuators because of the intended
applications.
The two isolators are effective, but they are based on an active control system,
whose complexity is a major drawback in the context of space applications. The
present study aims at simplifying the interface by reducing the on-board electronics: to this end, passive isolation with shunted transducers is investigated.
This chapter investigates the case of single-axis isolation; the construction of a
multi-axis isolator is presented in chapter 7.
6.2
Classical passive isolators
The simplest passive 1-d.o.f. isolator is presented in Fig. 6.1a; it consists of a
spring k and a viscous damper c connected in parallel. The mass m represents
a supporting structure that vibrates with amplitude Xn (sometimes called the
“noisy side”), and M represents a sensitive payload (the “quiet side”) with displacement Xq . The Transmissibility T is defined as the ratio between Xq and
Xn ; one easily finds, in Laplace variables:
87
88
sky
.
g
xq
Xq
M
M
m
àg xq
f
c
k
.
k
Xn
(a)
M
Xq
k
m
m
(b)
(c)
Xn
Figure 6.1: (a) Passive single-axis isolator. (b) Sky-hook isolator. (c) Equivalent
representation of the sky-hook.
T (s) =
Xq (s)
1 + 2ξs/ωn
=
Xn (s)
1 + 2ξs/ωn + s2 /ωn2
(6.1)
p
where ωn = k/M and ξ = c/2ωn M are the corner frequency and damping ratio
of the system, respectively. It is important to distinguish between the corner
frequency of the system and its natural frequency; ωn actually corresponds to
the natural frequency of the system when Xn is mechanically clamped.
|T (jω)| is shown
√ in Fig. 6.2 for various values of the damping ratio ξ. The
frequency ωc = 2ωn separates the region were |T (jω)| is greater than one (amplification) from the region where it is smaller than one (isolation). The amplification at resonance is governed by the damping ratio: the higher ξ, the lower
the amplification at ωn . The high-frequency attenuation rate, on the other hand,
is maximal when there is no damping (ξ=0); from Eq. 6.1 it corresponds to an
attenuation of ∼ 1/s2 , i.e. -40dB/dec, and it decreases to ∼ 1/s (-20dB/dec)
when damping is introduced. This conflict motivated the use of an active control
law, which should operate such as to simultaneously achieve a small overshoot
and a -40dB/dec attenuation rate, as represented by the dotted line in Fig.6.2.
6.3
Sky-hook damper and IFF
The sky-hook damper (Karnopp and Trikha, 1969) is an active isolation system
that reduces the amplification at ωn without deteriorating the high-frequency
isolation. It is represented in Fig. 6.1b: it consists of a spring k (no damper)
and a force actuator f acting in parallel. The feedback strategy consists in
generating a control force proportional to the absolute velocity of the payload,
6.3 Sky-hook damper and IFF
dB
20
89
xq
xn
ø=0
0
-20
ø1
ø2 > ø1
Objective of the
active isolation
-40
1
2
!=! n
10
Figure 6.2: Transmissibility of a passive isolator for various values of the damping
ratio ξ.
f = −gsXq (s). From the payload point of view, this is equivalent to connecting
the payload to a fixed point in space with a viscous damper of constant g (hence
the name “sky-hook”, Fig. 6.1c). The open-loop transfer function is:
sXq
ms
=
2
f
M ms + k(M + m)
(6.2)
and the root locus of the closed-loop system is shown in Fig. 6.3; the closed-loop
poles move on a circle. The transmissibility of the active isolator is:
·
¸−1
Xq (s)
M 2 g
T (s) =
=
s + s+1
Xn (s)
k
k
(6.3)
which exhibits an attenuation rate of -40 dB/dec at high frequency. The feedback
gain can be adjusted in such a way that the isolator is critically damped; in this
way the transmissibility exactly follows the objective represented in Fig. 6.2, as
there is no amplification at resonance and a maximal high-frequency attenuation
rate. Note, however, that the high-frequency slope is reduced to -20dB/dec when
viscous damping is introduced: the sky-hook damper is thus more effective when
applied to undamped systems, which has important consequences for the actual
implementation of the isolator.
Many different implementations of the sky-hook isolator exist; in most cases the
absolute velocity of the payload is measured with a geophone or an accelerometer.
90
Im
G(s)
H(s)
ms
m M s + k (m+M)
f
g
sXq
2
Re
(2 zeros + 1 pole)
Figure 6.3: Root locus of the sky-hook damper.
An alternative, shown in Fig. 6.4, consists in replacing the velocity feedback by
a force feedback based on the total force F transmitted by the isolator. Both
implementations are equivalent when the structures are rigid, because in this
case the payload acceleration is proportional to the force F transmitted by the
interface. The situation is different, however, if the two structures are flexible.
It can be shown that the open-loop FRF F/f , unlike that of acceleration or
velocity feedback Xq /f , always has alternative poles and zeros: as a result the
Integral Force Feedback control law has guaranteed stability (Preumont et al.,
2002). This fact motivated the use of force sensors in previous isolation works
developed at the ULB. Note that the guaranteed stability only holds as long as
perfect actuators and sensors are assumed; the actuator and sensor dynamics
must be accounted for in a full stability analysis.
xq
k
disturbance
source
F
sensitive
equipment
f
xn
IFF
Figure 6.4: Two arbitrary flexible structures connected by a single-axis soft isolator with force feedback.
6.4 Passive shunts
non-metallic
support
91
Soft iron
copper
wire
Xq
permanent
magnet
(NdFeB)
M
I
fc
k
Ysh
V
Xn
a)
b)
Figure 6.5: a) Typical construction of an electromagnetic transducer; the direc−
→
tion of the magnetic flux density B is also indicated. b) Single-axis isolation
system with a shunted electromagnetic transducer.
6.4
6.4.1
Passive shunts
Principles
A typical electromagnetic transducer is represented in Fig. 6.5a: the coil moves
−
→
perpendicular to the magnetic flux density B . Fig. 6.5b shows the insertion of
this transducer into a single-axis isolator; just as with the IFF, no viscous damper
has been added, because it would be detrimental to the high-frequency isolation1 .
−
→
When the coil moves with respect to B , an electromotive force V (in Volts) is
created in the coil; it is given by:
V = Tv (Ẋq − Ẋn )
(6.4)
with Tv = 2πnrB the transducer constant in V s/m (n is the number of turns in
the coil, r its radius and B the mean intensity of the radial component of the
magnetic flux density. Tv is also the constant (in N/A) relating the current I
circulating in the coil and the total force fc produced by the coil:
fc = Tv I
1
(6.5)
For the same reason, the isolator should be designed so as to minimize eddy currents damping; in particular, the support of the coil in Fig. 6.5a should be made of non-metallic material.
92
The dynamic equations governing the system of Fig. 6.5b are, in Laplace form:
¡
¢
(6.6)
M s2 + k Xq = kXn + fc
I = −Ysh (s)V
(6.7)
where the electrical resistance Rc and the self inductance Lc of the coil have
been included in the electrical admittance Ysh of the shunt. Combining Eq. 6.4
to Eq. 6.7, it is found that the poles of the system satisfy the characteristic
equation:
M s2 + Tv2 Ysh (s) s + k = 0
(6.8)
and that the transmissibility T (s) is given by:
T (s) =
6.4.2
Xq
Tv2 Ysh (s) s + k
(s) =
Xn
M s2 + Tv2 Ysh (s) s + k
(6.9)
Resistive shunts
If the shunt circuit is purely resistive, one has Ysh = 1/R, and thus, from Eq. 6.4,
6.5 and 6.7:
T 2s
(6.10)
fc = − v (Xq − Xn )
R
where R includes the resistance of the shunt circuit as well as that of the coil2 :
R = Rsh + Rc
(6.11)
Eq. 6.10 indicates that R-shunted transducers behave like viscous dampers of
constant c = Tv2 /R. This property has often been used in the past when trying
to damp a structure by short-circuiting the coil; in that special case Rsh = 0, and
Rc should be as low as possible to enhance the viscous damping.
In the context of shunted voice-coils, the coefficient Tv2 /Rc thus represents a factor
of merit of the transducer, as it measures the maximum damping action that can
be exerted by the transducer.
The transmissibility
for R-shunted systems is once again that of Fig. 6.2, with
√
ξ = Tv2 /(2R kM ); the usual trade-off between damping and high-frequency
isolation applies. A purely resistive shunt is thus not convenient for our purpose;
instead we would like the viscous coefficient c to be frequency-dependent, i.e.
large near ωn (so as to damp the peak) and small beyond ωn (so as to keep the
-40dB/dec isolation slope), as illustrated in Fig. 6.6 .
2
The inductance Lc of the coil can almost always be neglected with respect to its resistance
Rc , at least for frequencies below 1kHz.
6.4 Passive shunts
93
TdB
Large
damping
Small damping
so as to keep the
-40dB/dec slope
!n
!
Figure 6.6: Objectives for the viscous damping in the isolator.
The damping force fc is proportional to the current I in the coil: such a frequencydependent damping can thus be achieved by shaping the admittance of the shunt
Ysh , such that Ysh is large near ωn , and small beyond. This low-pass behavior
can be achieved passively, with the series RL or RLC circuits described in §6.4.3
and §6.4.4, or actively, as described in §6.6. Note that, to effectively damp the
resonance mode, the admittance Ysh does not only need to be large near ωn , but
also real (i.e. resistive-like).
6.4.3
First-order (RL) shunts
(a) Equivalent system
Let us connect a series RL shunt to the coil, as in Fig. 6.7a. The admittance of
the shunt is:
1
Ysh (s) =
(6.12)
Ls + R
where R and L include Rc and Lc , the intrinsic resistance and inductance of the
coil; Ysh is a first-order low-pass filter with a cut-off frequency ωe = R/L. From
Eq. 6.4, 6.5 and 6.7, the force fc exerted by the transducer is:
fc = −
Tv2 s
(Xq − Xn )
Ls + R
(6.13)
which is equivalent to that exerted by a spring of stiffness k1 and a dash-pot
of constant c connected in series as in Fig. 6.7b (compare with the system in
Fig. 6.1a); indeed such a mechanical system gives:
fc = −
k1 cs
(Xq − Xn )
cs + k1
(6.14)
94
Xq
Xq
M
c = T 2v=R
fc
k
L
Xn
k 1 = T 2v=L
M
c
k
k1
Xn
a)
b)
Figure 6.7: (a) isolator with an RL shunt; (b) equivalent mechanical system.
and the two systems are equivalent provided that k1 and c are given by:
k1 = Tv2 /L
(6.15)
c = Tv2 /R
(6.16)
(b) New corner frequency Ωn
The inductance L has been introduced in the circuit in order to limit the current
I in the coil (and thus the structural damping) at frequencies above ωe = R/L.
A side-effect of this insertion is the increase in the corner frequency; this property
is best understood with the equivalent mechanical representation of Fig. 6.7b, in
which L is modelled by a spring k1 (the lower L, the higher k1 ).
In this work, the increased corner frequency (i.e. that when the transducer is
shunted by an inductance L) is denoted Ωn ; it is most easily computed by replacing the transducer by a stiffness k1 = Tv2 /L in the model of the structure. In the
case of single-axis isolators, Ωn can be found from Eq. 6.8, which becomes (with
Ysh = 1/Ls):
M Ls2 + (Tv2 + kL) = 0
(6.17)
and thus:
Ω2n
µ
¶
µ
¶
Tv2 + kL
Tv2
k1
2
2
=
= ωn 1 +
= ωn 1 +
ML
kL
k
(6.18)
(c) Damping
The poles of the isolator with a general RL shunt can be found from Eq. 6.8,
which, combined with Eq. 6.12, becomes:
M Ls3 + M Rs2 + (Tv2 + kL)s + kR = 0
(6.19)
6.4 Passive shunts
95
øimax
Ò n= !n
!n =
nà! n
ø max
= Ò2!
i
n
q
2
Tv
1 + kL
p
k=M
Figure 6.8: Root locus of the RL shunt (L is fixed, R varies from 0 to +∞).
or:
1+
R s2 + ωn2
=0
L s(s2 + Ω2n )
(6.20)
where Eq. 6.18 has been used. The root locus of Eq. 6.20 is identical to that of
the IFF (Eq. 3.20) or of the piezoelectric R shunt (Eq. 4.25); it is reproduced
once more in Fig. 6.8. As in the previous cases, the maximum damping is given
by
max
ξRL
=
and it is achieved for
³
Ωn − ωn
2ωn
ωn ≥
Ωn ´
3
Ω2
opt
RRL
=√ n L
ωn Ωn
(6.21)
(6.22)
Note that, by changing the value of L, the designer has a certain amount of
influence on the ratio Ωn /ωn (Eq. 6.18), and thus on the maximal attainable
damping; this is not the case with piezoelectric shunt damping, in which that
ratio is fixed and generally very close to one. There is, however, a conflict between
damping and high-frequency isolation, as explained in the next paragraph.
(d) Transmissibility
From Eq. 6.12 and Eq. 6.9, the transmissibility with a RL shunt is:
TRL (s) =
=
(Tv2 + kL) s + kR
M Ls3 + M Rs2 + (Tv2 + kL) s + kR
R 2
L ωn
2
Ω2n s + R
L ωn
Ω2n s +
s3 +
R 2
Ls
+
(6.23)
(6.24)
96
Unlike resistive circuits, RL circuits allow a high-frequency attenuation rate of
∼ 1/s2 , i.e. -40dB/dec, but the corner frequency has increased (from ωn to Ωn ),
which negatively impacts the isolation. Fig. 6.9a shows the evolution of TRL
when R varies from 0 to +∞ and L remains constant. R only influences the
damping: it has no influence on the high-frequency transmissibility. The curve
with optimal damping is obtained when R = Ropt is chosen according to Eq. 6.22.
When R → ∞ and R → 0, TRL becomes, respectively:
Toc (s) =
ωn2
s2 + ωn2
and
TL (s) =
Ω2n
s2 + Ω2n
(6.25)
Fig. 6.9b, on the other hand, presents TRL for various values of L; R is each time
optimally chosen according to Eq. 6.22. Fig. 6.9b illustrates the conflict between
attenuation of the resonance mode and high-frequency isolation: lower values of
L lead to smaller amplification at resonance, and to a higher transmissibility at
high-frequencies. The penalty in high-frequency isolation can be assessed with:
µ
¶
TRL (jω)
Ω2n
Tv2
lim
= 2 = 1+
(6.26)
ω→∞ Toc (jω)
ωn
kL
as indicated in Fig. 6.9
6.4.4
Resonant (RLC) shunts
The addition of a capacitor C in series
√ with the RL circuit creates a resonance
at the electrical frequency ωe = 1/ LC, which, if properly tuned, can increase
the damping of the system. On the other hand, it does not change the highfrequency response of the system, because capacitors behave like short-circuits at
high frequencies.
Different optimisation objectives can be used to choose the values of the components. In this work, two methods have been investigated: the root locus analysis
and the H∞ norm minimization.
(a) Root locus analysis
The admittance Ysh (s) is:
s
1
s
=
(6.27)
2
+ Rs + 1/C
L s + 2ξe ωe s + ωe2
√
where we have defined the electrical frequency ωe = 1/ LC and damping ξe =
R/2ωe L. Introducing Eq. 6.27 into Eq. 6.8 and using Eq. 6.18, one gets the new
Y (s) =
Ls2
6.4 Passive shunts
dB
xq
xn
97
R=0
(Ò n)
R=1
(! n)
R opt
0
(Ò2n=!2n)dB
-20
-40
1
a)
dB
10
!=! n
xq
xn
0
L1
L2 > L1
-20
-40
1
b)
!=! n
10
Figure 6.9: RL shunt: transmissibility Xq /Xn with a RL shunt for various values
of R and L. (a) R varies while L does not change; (b) L varies, R is optimally
chosen according to Eq. 6.22.
98
Im
p1
RL shunt
Òn
Q
!n
p2
Optimal
Damping
Re
à !n
Figure 6.10: Root Locus of a RLC shunt with ωe = ωn .
expression for the characteristic equation of the system:
s4 + 2ξe ωe s3 + (ωe2 + Ω2n )s2 + 2ξe ωe ωn2 s + ωn2 ωe2 = 0
(6.28)
which can be rearranged in a root locus form:
¡
¢
s s2 + ωn2
1 + 2ξe ωe 4
=0
s + (ωe2 + Ω2n )s2 + ωe2 ωn2
(6.29)
This root locus is shown in Fig. 6.10 (with ωe = ωn ); that for a RL shunt is also
shown for comparison.
Eq. 6.29 is identical to that of a piezoelectric structure shunted by a parallel RL
circuit (Eq. 4.41): the analysis and conclusions developed in §4.3 therefore also
apply here. Two pairs of poles p1 and p2 are present in the system; each of them
follow a different loop. For a unique value of ωe , however, these two loops touch
each other in Q (Fig. 6.10): this double root is achieved for
s
ωeopt = ωn
and
ξeopt =
Ω2n − ωn2
ωn2
(6.30)
which maximizes the damping of both p1 and p2 and corresponds to:
opt
CRLC
=
1
ωn2 L
and
p
opt
RRLC
= 2 Ω2n − ωn2 L
(6.31)
6.4 Passive shunts
99
The damping at Q, i.e. the maximum attainable damping, is given by:
s
1
Ω2n
max
−1
ξRLC
=
2 ωn2
(6.32)
Fig. 6.11 shows the corresponding transmissibility. The curve corresponding to
R = 0 is also shown, which clearly shows the two pairs of poles p1 and p2 .
These curves are compared with the transmissibility of an optimal RL shunt
(corresponding to the same L and the value of R given by Eq. 6.22); as expected,
the addition of a capacitance does not change the high-frequency transmissibility.
dB
xq
xn
p2
!n
p1
RLC shunt (R=0)
RL shunt
0
-20
RLC shunt
(maximum damping)
B
A
Open-loop
-40
1
!=! n
10
Figure 6.11: Transmissibility Xq /Xn with RLC shunts. Results with an optimal
RL shunt are also shown for comparison.
(b) H∞ minimization
Instead of maximizing the structural damping ratio, one can choose to minimize
the H∞ norm of the transmissibility:
n
o
min {kT (jω)k∞ } = min max |T (jω)|
(6.33)
ω
The methodology is identical to that used by Den Hartog to optimise mechanical
Tuned Mass Dampers (TMD) (Den Hartog, 1956; Asami et al., 2002). It is based
on the fact that two points, denoted A and B in Fig. 6.11, are independent of
the electrical damping ξe : for a given value of C and L, all the transmissibility
100
curves cross each other in A and B. The solution of the problem is:
r
3p 2
1
opt
opt
CRLC = 2
and
RRLC =
Ωn − ωn2 L
ωn L
8
(6.34)
The optimal values for the capacitance C given by Eq. 6.31 (maximization of the
damping ratio) is identical to that given by Eq. 6.34 (minimization of the H∞
norm of T ); the optimal values for the resistance R, however, differ by 40%. Both
methods are compared in Fig. 6.12: the difference between the two curves is not
substantial, which indicates that the performances of the shunt are quite robust
with respect to variations of R.
dB
xq
xn
-20
A
B
RLC shunt
H norm
8
0
RLC shunt
maximum damping
Open-loop
-40
1
!=! n
10
Figure 6.12: Transmissibility Xq /Xn with a RLC shunt: first, when R and C are
chosen so as to maximize the damping ratio; next, when R and C are chosen so
as to minimize the H∞ norm of T .
6.5
6.5.1
Experimental set-up
Isolator
The foregoing theory has been experimentally tested on the single-axis setup
shown in Fig. 6.13. The isolator is placed between two beams whose rotations θ1
and θ2 create the vertical displacement of, respectively, the quiet and noisy sides;
these displacements are measured with two accelerometers, one B&K 4379 and
one DJB A/21, both of them approximatively 300pC/g. Two masses are placed
6.5 Experimental set-up
101
accelero 1:
quiet side
counter-weight 1
bearing 1
flexible joint
force sensor
(optional)
ò1
Carbon Fiber
stinger
counter-weight 2
flexible
membrane
(axial spring)
bearing 2
ò2
accelero 2:
noisy side
magnetic circuit
Electromagnetic
shaker
moving coil
Figure 6.13: Single-axis isolation system with a moving-coil transducer.
on the right side of the beams so as to balance the system; the setup is excited
by means of an electromagnetic shaker (B&K 4810) attached to the noisy side.
The architecture of the isolator follows closely that developed during previous
work at the ULB; it is also described in more detail in chapter 7. The coil is
centered inside the magnet by means of a flexible membrane, which also provides
the axial stiffness (k in Fig. 6.5b). The isolator is connected to the upper side by
a flexible joint that approaches the behavior of rotational hinges and thus allows
some rotation between the leg and the beam. In this work, a dedicated design
of the transducer with a large transduction coefficient Tv2 is used, as explained in
the next paragraph.
Although not essential, a force sensor B&K 8200 was also placed to allow the
comparison with Integral Force Feedback.
102
Non-magnetic
screw
non-metallic
support
Coil 1
(92 turns)
!
à
B
Coil 2
(161 turns)
!
à
B
(a)
(b)
Figure 6.14: Electromagnetic transducer. (a) Simplified representation. Dark
grey: magnets; light grey: soft iron. The direction of the magnetic flux density
−
→
B is also indicated. (b) Magnetic field lines (FE modelling with FEMM).
6.5.2
Transducer
The moving-coil transducers previously used at the ULB cannot realistically be
used with shunt circuits, because their Tv2 coefficients are too small. A new
transducer with an improved Tv2 coefficient was thus designed and built for the
purpose of this work; the design as well as the construction were performed at
the ULB. The design of the transducer was optimized in such a way that, with
the required level for Tv2 , the resistance of the coil Rc is minimal. Indeed, if Rc is
larger than the optimal shunt resistance (Eq. 6.22, Eq. 6.31 or Eq. 6.34), optimal
damping of the structure can no longer be attained.
The new transducer, schematized in Fig. 6.14a, is very similar to the commercially
available BEI-Kimco LA15-16-024A, but the gap in which the coil moves has been
enlarged and the coil and magnetic circuit have been optimized. It is made of two
Neodymium-iron-boron (NdFeB) permanent magnets (φe = 26mm, φi = 8mm,
height=10mm) placed with opposite magnetization directions, a magnetic circuit
in soft iron (height: 30mm, φi = 36.4mm, φe = 41.4mm), and two coils made of
copper wire (φ = 0.4mm, 92 and 161 turns respectively). The coils are 2.4mm
thick (6 layers of wire). The support of the coil is made of non-metallic material
103
to avoid eddy currents, and the gap in which the coil moves is 5.2mm wide (4mm
in the upper part of the system). The screw maintaining the magnets and the
magnetic circuit is made of a non-magnetic material. From measurements, the
transduction constant Tv is approximatively 9.93 N/A, the resistance of the coil
Rc is 3.41Ω and its inductance Lc is 0.75mH.
A magnetic FE model of the transducer was created with the freeware “FEMM”
(Finite Element Method Magnetics, http://femm.foster-miller.net); the magnetic
field lines are shown in Fig. 6.14b. This model predicts a nominal Tv of 9.76 N/A,
and a resistance Rc of 3.44 Ω, both of which are very close to the experimental
values. The linearity of the transducer with respect to the axial position of the
coil was investigated with the same FE model: it was found that Tv decreases
by 2.2% when the coil translates 1mm upwards, and by 1.2% when it translates
1mm downwards.
6.5.3
Passive components
Figure 6.15: Passive inductors (47mH and 6.8mH) and capacitors (4.7mF and
10mF), respectively.
From simulations, the required shunt inductance L and capacitance C are of
the order of 100mH and 10mF , respectively. Although these values are fairly
high compared with the ones usually introduced in electronic circuits, they can
still be attained with passive components. Companies such as Epcos, Schaffner
or Wurth sell suitable inductors (chokes) for a few euros, and it is possible to
find aluminium electrolytic capacitors of appropriate values with companies such
as Vishay BC Components or BHC Components. Fig. 6.15 shows a few of the
components that are used in this work. These cheap components are not designed
to be extremely precise: their actual value can differ largely from their nominal
value. In all cases the actual values of the components have been verified with
an Agilent 4294A impedancemeter. Note that, because of non-linearities in the
104
L
49mH
220mH
Ropt
(RL shunt)
4
10.5
Ropt
(RLC shunt)
1.5
3.2
Rinductor
Rc
1.5
4.3
3.4
3.4
Table 6.1: Optimal shunt resistance for two values of the shunt inductance L.
The resistance introduced by the inductor is also shown, along with the intrinsic
resistance of the coil Rc . All the values are in ohms.
magnetic circuit, these values also change with the amplitude of the current and
with the frequency.
A special attention must be paid to the series resistances introduced by these
components: these parasitic resistances add to that of the coil Rc and, if the sum
exceeds the optimum value defined in Eq. 6.22, Eq. 6.31 or Eq. 6.34, optimal
damping of the structure cannot be attained. The inductors used in this work
have a nominal ratio R/L between 20Ω/Hand 30Ω/H; lower ratios can be obtained, but at the expense of larger, more expensive inductors. The electrolytic
capacitors, on the other hand, typically introduce 10-20mΩ.
6.5.4
Table 6.1 shows the optimal values of the shunt resistance, obtained from Eq. 6.22
and Eq. 6.34, for the RL and RLC (H∞ norm) shunts and for two values of L
(49mH and 220mH); notice the lower values for the RLC shunt. The resistance
of the coil Rc and the series resistance Rinductor introduced by the inductor are
also indicated; the parasitic series resistance introduced by the capacitors can, in
this case, be neglected.
The experimental transmissibility T = Xq /Xn with a RL shunt, obtained with a
HP35670A Fourier Analyzer, is shown in Fig. 6.16. When the 220mH inductor
is used, the sum of Rinductor and Rc is lower than the optimal resistance Ropt
(Table 6.1), which is why a small resistor was inserted such that the curve is
optimally damped. With the 49mH inductor, the sum of Rinductor and Rc slightly
exceeds Ropt and no resistor was introduced.
The experimental results with RLC shunts are shown in Fig. 6.17. The inductors
are the same as those of Fig. 6.16, and the capacitors were chosen according to
Eq. 6.34, though a little trial and error was needed to account for the imprecision
of the components values. The sum of Rinductor and Rc far exceeds Ropt , which
explains why the curve with L = 49mH is only slightly more damped than
the corresponding curve with a RL shunt. The situation is slightly better with
L = 220mH, however, because the optimal resistance is proportionally larger:
the attenuation of the resonance peak is more pronounced than that with a RL
shunt, and the double peak typical of a RLC shunt can be seen.
105
40
20
ì ì
ìXq ì
ìXnì
RL
dB
L=220mH
L=49mH
0
-20
-40
1
Hz
10
100
Figure 6.16: Experimental Transmissibility with RL shunts (in dashed: theoretical results).
40
20
ì ì
ìXq ì
ìXnì
RLC
dB
L=220mH
0
L=49mH
-20
-40
1
10
Hz
100
Figure 6.17: Experimental Transmissibility with RLC shunts (in dashed: theoretical results).
106
6.6
Active shunts
I
mechanical
structure
Istru
Rc
Lc
I
fc
V
Vstru
Ish
Ysh
Istru
à
Z structure Vstru
(Vstru /Istru )
Ish
Ysh
Figure 6.18: Feedback representation of a mechanical structure with a shunted
moving-coil transducer.
Section 6.4.2 and Fig. 6.6 stress that the shunt admittance Ysh (s) should be large
near ωn , so as to reduce the amplification at resonance, and small above ωn , so
as to enhance the high-frequency isolation. The admittance of any passive shunt,
however, cannot decrease by more than -20dB/dec at high frequencies3 which,
as shown in the previous sections, increase the corner frequency (from ωn to Ωn )
and negatively impacts the high-frequency isolation (see e.g. Eq. 6.26).
To avoid this, admittances with a larger attenuation rate (-40dB/dec or more)
are required; such admittances however require an active implementation, and
can thus potentially destabilize the system. Similar to what was done in chapter 5 with piezos, the stability of the shunted structure can be assessed with
the feedback diagram of Fig. 6.18. V is the electromotive force (in Volts) created in the coil by the magnetic field, Rc and Lc are the resistance and inductance of the coil, respectively, and Vstru is the voltage across the shunt circuit.
Zstructure = Vstru /Istru is the electrical impedance of the structure seen from the
terminals of the coil; it includes the impedance of the structure V /Istru as well
as that of the coil (Rc + Lc s) and can be obtained either from simulations or
from measurements. Note that Zstructure does not roll-off at high-frequencies, because of the Rc and Lc components: Ysh must therefore have some high-frequency
roll-off in order to decrease the risk of spillover instability.
6.6.1
Active admittance simulator
An active electronic circuit that emulates the behavior of a general admittance
Ysh (s) has been designed and built by the company Micromega Dynamics s.a. Its
3
because, being passive, its phase must always remain within [− π2 , π2 ] and thus, from the first
Bode integral, the high-frequency slope remains within [-20dB/dec, +20dB/dec].
6.6 Active shunts
+
107
IL
current
source
-
Ysh(s)
V
ZL
(b)
(a)
Figure 6.19: (a) Simplified diagram of the admittance simulator and (b) its actual
implementation (17x10 cm).
principle is shown in Fig. 6.19a; it follows directly from the feedback scheme of
Fig. 6.18. A voltage-controlled current source drives the load ZL (the transducer
in this case); the voltage V across the load is simultaneously measured and sent
through the filter Ysh (s), whose output controls the current source. The system
behaves “as if” the load ZL was connected in parallel to a circuit of admittance
Ysh (s).
The actual implementation of the electronic circuit is shown in Fig. 6.19b. Ysh (s)
is implemented, with a 20kHz sampling frequency, by a DSP processor integrated
on the board. The parameters of the filter can most easily be modified by means
of a temporary connection with a PC and a dedicated software; the connection
is no longer required after the modification as the parameters are stored in an
integrated flash memory.
6.6.2
Many different active shunts can be employed: the isolation performances are
preserved as long as their high-frequency roll-off is greater than -20dB/dec. For
convenience, in this work we use low-pass Butterworth filters, i.e. filters whose
transfer function is given by (see e.g. Deliyannis et al., 1999):
H(s) =
A
(s − s1 )(s − s2 ) · · · (s − sn )
(6.35)
where n is the order of the filter and the poles s1 . . . sn symmetrically lie on the
left part of a circle whose radius is ωc , with ωc the cut-off frequency of the filter. Butterworth filters are often called “maximally flat” filters, because their
frequency responses are as constant as mathematically possible (no ripples) in
108
References
the passband4 . In this work we used filters of order 3 and 4; extensive simulations showed that higher-order filters or other filter architectures do not perform
significantly better.
The parameters A and ωc of the Butterworth filters were optimized so as to
minimize the H∞ norm of the transmissibility while keeping a gain margin of
2 and a phase margin of 45◦ . Experimental results are shown in Fig. 6.20; the
Nyquist plots of the corresponding open-loop transfer functions (in the sense of
Fig. 6.18, i.e. Zstructure · Ysh , where Zstructure is measured and Ysh is simulated)
are shown in Fig. 6.21.
An experimental transmissibility with a sky-hook damper, implemented with an
IFF control law, is also shown for the purpose of comparison. The Butterworth
shunts, unlike the passive RL or RLC shunts, allow the suspension modes to be
damped without deteriorating the high-frequency isolation: compare Fig. 6.20
with Fig. 6.16 or Fig. 6.17. They however introduce less damping than the skyhook damper, which can achieve critical damping. Besides, their stability is not
guaranteed and must be verified on a case-by-case basis, in contrast to the IFF.
For these reasons, isolation with active shunts was not investigated further.
6.7
References
T. Asami, O. Nishihara, and A.M. Baz. Analytical solutions to H∞ and H2 optimization of dynamic vibration absorbers attached to damped linear systems.
ASME J. of Vibration and Acoustics, 124:284–295, April 2002.
CRC Press, 1999.
J.P. Den Hartog. Mechanical Vibrations. McGraw-Hill, New-York, 4th edition,
1956.
D.C. Karnopp and A.K. Trikha. Comparative study of optimization techniques
for shock and vibration isolation. Trans. ASME Journal of Engineering for
Industry, series B, 91(4):1128–1132, 1969.
A. Preumont, A. François, F. Bossens, and A Abu-Hanieh. Force feedback versus acceleration feedback in active vibration isolation. Journal of Sound and
Vibration, 257(4):605–613, 2002.
4
the first 2n − 1 derivatives of the frequency response are zero at ω = 0.
References
109
jTj (dB)
3rd order
Open-Loop
20
4th order
0
IFF
-20
-40
-60
10
! (Hz)
100
Figure 6.20: Experimental transmissibility with active shunts (Butterworth filters
of various orders); results with IFF are also shown for comparison.
4th order
3
2
3rd order
1
0
1
-1
2
3
-1
Figure 6.21: Nyquist plots corresponding to the active shunts used in Fig. 6.20.
110
References
300:644–661, 2007.
Chapter 7
Multi-axis isolation
7.1
Introduction
To fully isolate two rigid bodies with respect to each other, six single-axis isolators
must be located judiciously. An attractive architecture is that of a Gough-Stewart
platform, which consists of 6 identical single-axis isolators connected to the end
plates as shown in Fig. 7.1 (Gough and Whitehall, 1962, or Stewart, 1965-66; for
a history of the invention, see e.g. Bonev, 2003).
A series of such isolators has been built for space applications, mainly in the
USA (Spanos et al., 1995; Rahman et al., 1998; McInroy et al., 1999; Thayer
et al., 1998, 2002; Hauge and Campbell, 2004). Most of these systems are based
on a cubic architecture proposed by Gough and further developed by Geng and
Haynes (1994), where the active struts are arranged in a mutually orthogonal
configuration connecting the corners of a cube (Fig. 7.2). This topology provides
a uniform control capability and a uniform stiffness in all directions, and it minimizes the cross-coupling among actuators and sensors of different legs (being
orthogonal to each other).
Two prototypes, also based on the cubic configuration, were successively built at
the ULB, respectively in 2002 and 2004. The former was part of a PhD thesis
(Abu Hanieh, 2003), and the latter, sketched in Fig. 7.1, is described in Preumont
et al. (2007) and in this chapter (§7.2). The main improvement of the second
prototype over the first one is that the mass of the leg has been reduced drastically.
This in turn increases considerably the natural frequency of the local modes of
the leg, which, as shown below, has a large impact on the isolation performances.
Both prototypes were based on a decentralized IFF control law implemented with
electromagnetic actuators, as suggested in chapter 6. They were successfully
tested in micro-g during a parabolic flight test campaign; besides the two above111
112
Payload plate
(quiet side)
Legs
(single axis
isolators)
Base plate
(noisy side)
Figure 7.1: Multi-purpose isolator based on a Gough-Stewart platform with cubic
configuration.
zb
zb
5
5
4
6
4
4
5
7
3
5
yb
6
6
2
6
1
xr
1
2
xb
1
xb
node 0 : (0,0,0) node 4 : (0,L,L)
node 1 : (L,0,0) node 5 : (0,0,L)
node 2 : (L,L,0) node 6 : (L,0,L)
node 3 : (0,L,0) node 7 : (L,L,L)
node 8 : (L/2, L/2, L/2)
3
yr
8+
8
3
0
4
Payload
Plate
Base
Plate
3
2
1
yb
2
z r station of payload plate = L/2 3
zr station of base plate = - L/2 3
Figure 7.2: Geometry and coordinate system for the cubic hexapod isolator.
Numbers in bold indicate the struts.
7.2 Active isolator
113
mentioned publications, more information is available in de Marneffe et al. (2004),
and in Avraam et al. (2005).
The construction of a multi-axis isolator, whether active or passive, is a delicate
task involving careful mechanical design and numerous optimization processes.
The first part of this chapter (§7.2) presents the mechanical design and modelling
of the 2004 prototype, including the various components of the six legs and the
assessment of the transmissibility. A second part (§7.3) presents the preliminary
results of an ESA-PRODEX research program, currently being conducted at the
ULB, which aims to develop a passive isolator with RL shunt circuits as suggested
in chapter 6.
7.2
7.2.1
Active isolator
Leg design
The membrane is also
used as a flexible
joint
Base
Base
plate
Plate
N
Flexible
joint
Load
cell
S
Mobile
Payload
plate
Plate
Figure 7.3: Design of the leg for the 2004 prototype.
Fig. 7.3 schematizes the design of the leg that has been considered for the 2004
prototype. The permanent magnet, the heaviest part of the leg, is attached to the
base plate. The membrane simultaneously maintains the coil inside the magnet,
introduces an axial compliance and is used as a flexible joint. The coil axis is
allowed to rotate with respect to the magnet axis, which necessitates an increase
of the gap between the coil and the magnet. The stinger, which is of carbon fibre
construction, is attached to the center of the membrane. It supports the voice coil
at one end, and is attached to the force sensor at the other end, which in turn is
connected to the payload plate by a single flexible joint. This configuration, unlike
that of the 2002 prototype, successfully passed launch vibration qualification tests
(LSSP, 2005). Fig. 7.4 shows an exploded view of the leg; some details of the
design follow.
114
Voice-coil
Magnet
Support
Magnet
Cover
Flexible
Joint
Membrane
Stinger
Load cell
Figure 7.4: Exploded view of the leg (2004 design).
a)
b)
c)
d)
e1)
e2)
Figure 7.5: various membrane geometries and FE mesh.
7.2 Active isolator
115
(a) Membranes
The membranes are made of Beryllium Copper alloy, a non-magnetic material
with high yield stress. A thin film coating was added to avoid corrosion due to
metal-metal interaction with the aluminium support. The membrane geometry
was optimized to (i) maximize the ratio between the radial stiffness and longitudinal stiffness, (ii) to minimize variation in radial stiffness with respect to
longitudinal extension of the leg, and to (iii) minimize stress concentration to
improve the fatigue life. Fig. 7.5 shows various membrane geometries which have
been tested during the course of this project. A Finite Element (FE) analysis
was performed to determine the various spring constants required for the global
model of the platform.
(b) Flexible joints
F.E. mesh
(Samcef field)
Figure 7.6: Flexible joint used in this work.
Ideally, the flexible joints should approximate a spherical joint; that is, they
should exhibit high axial and shear stiffness, and low bending and torsional stiffness. On the other hand, the joints also play a vital role in the mechanical integrity of the system, which calls for strong, and consequently stiff, joints. These
conflicting requirements have led to extensive numerical studies and prototyping.
Eventually, we opted for the design of Fig. 7.6, manufactured by electro-erosion.
The material selected was NiTiNOL alloy, which was chosen for its low Young
modulus, and high yield strength, respectively ∼ 60 GPa and 900-1900 MPa in
this case. In a later version, developed at Micromega Dynamics on behalf of
ESA/ESTEC (LSSP, 2005), Titanium was used instead of NiTiNOL, due to the
availability of more reliable material data. The joint profile was studied numer-
116
ically with FE, and a Guyan reduction was performed to determine the 12 × 12
stiffness matrix of the joint.
7.2.2
Closed-loop properties
For simplicity reasons, we take the view that six legs are identical, and that they
are controlled in a decentralized manner with the same gain. Compared with the
single-axis isolator of chapter 6, two new problems arise: (i) The system does not
have one, but six suspension modes, with generally different frequencies, and it
will not be possible to achieve critical damping simultaneously for all suspension
modes with a single gain. (ii) The flexible joints have a small rotary stiffness.
Although small, this residual rotary stiffness has a significant effect on the closedloop performance of the suspension, as explained below.
According to Abu Hanieh (2003), the dynamics of the isolator, when the base
plate is fixed, are governed by
M ẍ + (kBB T + Ke )x = Bu
(7.1)
where x = (x, y, z, θx , θy , θz )T contains the small translations and rotations of the
upper plate, evaluated at the geometrical center of the platform, u = (u1 , . . . , u6 )T
is a vector of active control forces in the legs, k is the axial stiffness of the
membranes, Ke is the stiffness matrix of the flexible joints, B is the projection
matrix mapping the local leg coordinates into the global coordinates, and M is
the 6 × 6 mass matrix of the payload, given by:
·
¸
mI6 0
M=
(7.2)
0
J
where m is the mass and J the inertia tensor of the payload in the payload frame.
y = (y1 , . . . , y6 ), the vector of the six axial forces in the six respective legs, is
given by:
y = u − kq = u − kB T x
(7.3)
Using a decentralized integral force feedback with the same gain g for every loop,
the control inputs are:
g
u = H(s)y = − y
(7.4)
s
(g is a scalar in this case). Combining Eq. 7.1, Eq. 7.3 and Eq. 7.4, one gets the
closed-loop characteristic equation:
M ẍ + (kBB T + Ke )x =
g
kBB T x
s+g
(7.5)
7.2 Active isolator
117
(a)
(b)
j! i
j! i
Figure 7.7: (a) Root locus of the suspension modes of the perfect six-axis isolator
(Ke = 0) with decentralized integral force feedback. (b) Effect of the stiffness of
the flexible joints (Ke 6= 0).
(a) Perfect joints
First, consider the case of perfect spherical joints, Ke = 0. In this case, Eq. 7.5
becomes
s
[M s2 +
(kBB T )]x = 0
(7.6)
s+g
The six suspension modes ωi (i = 1, . . . , 6) of the isolator are the solutions of
Eq. 7.6 for g = 0. If one denotes Φ the matrix of the suspension modes, normalized
in such a way that ΦT M Φ = I6 and ΦT (kBB T )Φ = diag(ωi2 ), Eq. 7.6 can be
transformed into modal coordinates according to x = Φz. In modal coordinates,
Eq. 7.6 is reduced to a set of decoupled equations:
s2 +
s
ω2 = 0
s+g i
(7.7)
s
=0
+ ωi2
(7.8)
or:
1+ g
s2
i = 1, . . . , 6. The corresponding root locus is shown in Fig. 7.7a: its open-loop
poles are at ±jωi , and its open-loop zeros are at the origin s = 0. The root locus
is identical to Fig. 6.3 for a single axis isolator; however, unless the 6 natural
frequencies of the suspension modes are identical, a given value of the gain g
leads to different pole locations for the various modes, and it is not possible to
achieve the same damping for all modes. Better, more balanced performance will
be achieved if ω1 to ω6 are close to each other. Thus, the payload should be
located in such a way that the modal spread ω6 /ω1 is minimized (Spanos et al.,
1995).
118
!5; !6
!4
!3
!1; !2
Figure 7.8: Typical root locus of a complete isolation system with real joints.
(b) Real joints
Let us investigate the influence of the parasitic stiffness Ke introduced by the
flexible joints. In this case, the closed-loop characteristic equation becomes
[M s2 + Ke +
s
(kBB T )]x = 0
s+g
(7.9)
The asymptotic solutions for high gain (g → ∞) are no longer at the origin s = 0,
but satisfy the eigenvalue problem
(M s2 + Ke )x = 0
(7.10)
The solutions to Eq. 7.10 are the natural frequencies, zi , of the system when
the axial stiffness of the strut approaches zero. This shift of the zeros from the
origin to finite frequencies, Fig. 7.7b, has a substantial influence on the practical
performance of the isolator, and motivated careful design of the joints.
The combined effect of the modal spread and the joint stiffness is illustrated in
Fig. 7.8. There are only 4 different loci because of the symmetry of the system. The bullets correspond to the closed-loop poles for a fixed value of g. The
sensitivity of the closed-loop poles to changes in g varies from locus to locus.
7.2.3
Fröbenius norm
The assessment of the multi-axis transmissibility is more complex than the singleaxis one; indeed the quiet side of the isolator as well as its noisy side now have
six d.o.f., and the transmissibility is a 6 × 6 matrix:
Xq (ω) = T (ω) Xn (ω)
(7.11)
7.2 Active isolator
119
with x = (x, y, z, θx , θy , θz )T the displacement vector of each side (measured at the
system geometrical center). To better interpret the performance of the isolator,
it is more convenient to define a scalar indicator with a meaning similar to that
of the transmissibility of a single-axis isolator. The Fröbenius norm is often used
for this purpose (Spanos et al., 1995); it is defined as:
³
h
i´1/2
kT (ω)k , trace T (ω) T (ω)H

1/2
6 X
6
X
=
|Tij (ω)|2 
(7.12)
(7.13)
i=1 j=1
where (.)H stands for the matrix Hermitian (i.e., the conjugate transpose). Physically, kT (ω)k represents the frequency distribution of the energy in the quiet side
when the six inputs of the base plate are uncorrelated white-noise with unity
spectral density (Preumont et al., 2007).
To better compare the multi-axis transmissibility with the single-axis one, we
introduce a small variation and consider instead:
√
Γ(ω) , ||T (ω)||/ 6
(7.14)
which, just as with single-axis systems, provides Γ|ω=0 = 1.
7.2.4
Model of the isolator
A Finite Element model (SAMCEF) of the complete isolator has been created;
it includes the dynamics of the legs and that of the upper plate, and takes the
stiffness of the flexible joints into account. The model of the joint is reduced to 12
d.o.f. by means of a Guyan reduction. The membrane, by contrast, is assumed
massless and reduced to 6 equivalent spring constants only (three in translation
and three in rotation). The stinger is modelled with beams elements, and the
load cell and voice coils are considered to be rigid and are introduced in the model
by means of a tensor of inertia. Once combined, all these reduced components
produce a leg model with less than 100 d.o.f. In a second step, the dynamic model
of the platform has been transformed into state-space using MATLAB, in which
the influence of the shunts is introduced with the feedback scheme in Fig. 6.18.
The numerical estimate of the Fröbenius norm of the 2004 prototype is presented
in Fig. 7.9. The modal spread ω6 /ω1 is 2.2; because of this modal spread, each
mode has a different damping when the control is turned on. The isolator is
effective in the range [10-400] Hz: beyond 400 Hz, the local dynamics of the legs
interact with those of the isolator which significantly impacts the transmissibility.
120
40
30
È(!)
6 suspensions modes
legs
dynamics
20
Transmissib ility (dB)
Without Control
10
Isolation range
0
With IFF Control
-10
-20
-30
-40
-50
1
10
100
Hz
500
Figure 7.9: Fröbenius norm of the transmissibility of the 2004 multi-axis isolator
(FE simulations).
Maximizing the frequency of the first local mode of the legs is a major challenge
in the design of a six-axis isolator with broadband isolation capability.
7.3
Passive isolator
The active isolator of 2004 was found to be very effective: it effectively isolates
between 10 Hz and 400 Hz, and the attenuation almost attains -40dB in a large
frequency range (Fig. 7.9). It however relies on an active control system, which
increases the complexity of the interface. This section summarizes the preliminary
results of an ESA-PRODEX research program, currently conducted at the ULB,
which aims to simplify the system by using passive shunt circuits instead. We also
try to enhance the isolation range by increasing as much as possible the natural
frequency of the first local mode of the leg. The following sections presents the
modification introduced in the design, with respect to the prototype of 2004, to
attain the foregoing objectives.
7.3.1
Mode shapes of the legs
The dynamics of the leg (2004 design) were analyzed with Finite Elements. Compared with the model described in §7.2.4, the flexible joint and the membrane
were not reduced but instead fully modelled with volume elements (∼20,000 d.o.f.)
7.3 Passive isolator
121
Load cell
inertia
Stinger
(CFC)
Voice-coil
inertia
(a)
(b)
(c)
Figure 7.10: Computed mode shapes of the legs; (a) local membrane mode, (b)
joint shear mode, (c) membrane shear mode.
122
and shell elements (∼30,000 d.o.f.), respectively. The upper face of the joint and
the external side of the membrane were clamped.
Various mode shapes are illustrated in Fig. 7.10a-c. Many “purely” membrane
modes (i.e., only the membrane moves, Fig. 7.10a) are present, starting from
300 Hz on; these modes cannot be avoided. They however have very little influence on the transmissibility as their modal mass is extremely low.
The first important mode appears around 400 Hz; it consists in a shear deformation of the joint (the membrane is not deformed, Fig. 7.10b). The natural
frequency is mainly governed by the mass of the upper part of the leg and by the
shear stiffness of the flexible joint; the influence of the membrane stiffness and
that of the voice-coil inertia are very limited. The next mode (around 850 Hz)
mainly consists in a shear deformation of the membrane (Fig. 7.10c), and the
third one (not shown), also around 850 Hz, is a vertical mode, i.e. the leg moves
along its axis.
7.3.2
Load cell
The load cell is relatively heavy (∼ 20 g, compared to a total mass of ∼ 60 g for the
leg) and therefore significantly influences the first natural frequency (joint shear).
As shunt circuits do not require the use of a load cell, the mass of the upper part
of the leg significantly decreases and the first natural frequency increases from
400 Hz to about 750 Hz. The membrane shear mode is little affected by this
change.
7.3.3
Flexible joints and membranes
The joints of the 2004 platform are made of NiTiNOL, a soft (∼ 60 Gpa) and
relatively dense (∼ 6450 kg/m3 ) alloy. The use of a stiffer, lighter alloy such as
Titanium (TiAlV: E=110 GPa and ρ=4100 kg/m3 ) was considered. FE simulations showed that this material can indeed raise the joint shear mode above
1000 Hz, but that the advantage is limited, because Titanium also increases the
6 corner frequencies ω1,...,6 ; this in turn limits the frequency region where the
isolation is effective. Moreover, the membrane shear mode around 850 Hz is not
affected by this change.
The same conclusions apply to the membranes: even if a stiffer membrane indeed
increases the frequency of the membrane-shear mode of the legs, it also increases
the frequency of the six suspension modes. For these reasons, it was decided to
keep the 2004 design of the joints and membranes.
123
+/- 2.4°
17.47
inner gap
0.9
26
outer gap
0.72
34.84
39.74
Figure 7.11: Effects of the coil misalignment (dimensions in mm).
7.3.4
Transducer
The transducer presented in §6.5.2 is effective but also bulky and relatively difficult to build, mainly because of the two coils and magnets. Simulations also
showed that the performances of this transducer are higher than what is actually
required, as a RL shunt can be implemented on a less efficient but simpler system.
Finally, the height of the coil support requires an unnecessary large clearance between the coil and the magnetic circuit, in order to allow some rotation to take
place between the leg and the base plate, as illustrated in Fig. 7.11.
For all these reasons, a new, simpler transducer with a single magnet has been
designed; it is shown in Fig. 7.12 (some of its dimensions are also shown in
Fig. 7.11). An extensive optimization procedure based on magnetic FE simulations1 was performed to ensure that, for the required value of Tv2 , the coil
resistance Rc be minimal. The permanent magnet is the same as those used in
chapter 6 (φi = 8mm, φe = 26mm, height=10mm). The nominal values of the
inner and outer gap are 0.9mm and 0.72mm, respectively, and the coil is 14.47mm
high, which allows a ±2.4◦ rotation between the coil and the magnet. The total clearance in the magnetic circuit is 4.4mm, and the coil is 2.8mm thick. A
mechanical stop is placed that prevents the angle from exceeding ±2.1◦ and the
axial translation ±2.5mm, such that the membrane and the coil are protected
1
with the freeware “FEMM”, http://femm.foster-miller.net.
124
CFC Stinger
mechanical
stop
magnetic
circuit
flexible
membrane
copper
wire
permanent
magnet
Figure 7.12: Final version of the transducer.
from excessive displacements. Simulations showed that these displacements are
sufficient, even when the unavoidable geometrical tolerances are taken into account. The coil is made of 114 turns of copper wire (6 layers, φ = 0.4mm). The
transduction constant Tv is 3.8 N/A, and the coil resistance Rc is 1.65 Ω. Just as
with the transducer of chapter 6, the comparison between predicted characteristics with the magnetic FE model and experimental measurements proved to be
quite good.
It must be noted that the mass and inertia properties of the transducer have little
impact on the first natural frequency of the legs (joint shear) and, thus, they have
little impact on the isolation range of the platform; the transducer can thus be
designed according to electrical and kinematic considerations only.
7.3.5
Upper plate
The upper plate of the 2004 prototype (Fig. 7.13a) has natural modes around
500 Hz, which is acceptable because it is higher than the first natural frequency
of the leg (∼400 Hz). In this project, however, the first natural frequency of
the legs has increased from 400 Hz to 750 Hz, which motivated a redesign of
the plate. Its triangular shape was changed into a more effective star-like shape
(Fig. 7.13a-b); the thickness was also increased from 20mm to 25mm. According
to numerical simulations, the first natural frequency of the new plate is 940 Hz,
125
which is consistent with the new leg design. A CAD view of the new passive
isolator is shown in Fig. 7.14.
(b)
(a)
Figure 7.13: (a) Upper plate (2004); (b) new version.
Figure 7.14: CAD view of the passive isolator
7.3.6
Numerical results
In this project we mainly consider the use of RL shunts. RLC shunts were discarded because they are resonant circuits with a usually very narrow bandwidth
126
References
and, thus, are not really suitable for simultaneously damping several suspension
modes. They also require a smaller coil resistance Rc than RL shunts (see Table 6.1), which means that the transducer is more difficult to build. The active
admittance simulator described in chapter 6 is not needed as it is possible to
attain our objectives with passive components.
The choice of the inductance L results from a trade-off, explained in chapter 6,
between the attenuation of the suspension modes and the values of the six corner
frequencies. In this case, simulations showed that L = 25mH is a reasonable
value; note that the intrinsic inductance of the coil Lc ∼ 0.75mH can almost
always be neglected with respect to L. The different contributions to the resistance of the circuit are shown in Table 7.1; the total exceeds the optimal resistance
Ropt = 1.85Ω of the shunt circuit, which is why no additional resistor is inserted.
inductor:
coil:
resistor:
total:
∼ 0.75
1.65
0
2.4
Table 7.1: The expected contributions (in Ohms) to the resistance of the RL
circuit.
Fig. 7.15 presents the Fröbenius norm of the transmissibility with these RL
shunts. For the purpose of comparison, the transmissibility with a purely resistive shunt is also shown; a resistor of 1.25Ω was chosen such that both RL
and R shunts have approximately the same amplification at resonance. The RL
shunt indeed allows a more effective isolation than the R shunt between 30Hz
and 700Hz.
Fig. 7.16 compares the performances of the passive isolator (RL shunts) with
those of the same isolator controlled by Integral Force Feedback. The IFF leads
to more attenuation of the 6 suspension modes and it does not increase the corner
frequencies of the system, but the weight of the load cells in the legs decreases
the frequency of the first local mode (the joint shear mode, see Fig. 7.10) and,
thus, limit the frequency range where the isolation is effective.
7.4
References
M. Avraam, B. de Marneffe, I. Romanescu, M. Horodinca, A. Deraemaeker, and
References
127
Transmissibility (dB)
40
È(!)
20
RL shunt
0
R shunt
-20
-40
-60
1
100
10
Hz
1000
Figure 7.15: Fröbenius norm of the transmissibility with R and RL shunts. Numerical simulations based on a FE model of the platform.
Transmissibility (dB)
40
È(!)
20
RL shunt
0
Active control
(IFF)
-20
-40
-60
1
10
100
Hz
1000
Figure 7.16: Numerical transmissibility (Fröbenius norm) with a passive RL
shunt and with an active control system based on the IFF.
128
References
A. Preumont. A six degrees of freedom active isolator based on stewart platform
for space applications. In 56th International Astronautical Congress (Paper
IAC-05-C2.201), Fukuoka, Japan, Oct. 2005.
I. Bonev. The true origins of parallel robots.
http://www.parallemic.org/Reviews/Review007.html, 2003.
B. de Marneffe, A. Abu Hanieh, M. Avraam, A. Deraemaeker, M. Horodinca,
I. Romanescu, and A. Preumont. A novel design of stewart platform for active
vibration isolation. 38th ESA parabolic flight campaign final report (Prodex90147), Oct. 2004.
Z.J. Geng and L.S. Haynes. Six degree-of-freedom active vibration control using
the stewart platforms. IEEE Transactions on control systems technology, 2(1):
45–53, March 1994.
V.E. Gough and S.G. Whitehall. Universal tyre testing machine. In Proc. Ninth
International Technical Congress F.I.S.I.T.A., 117, 1962.
G.S. Hauge and M.E. Campbell. Sensors and control of a space-based six-axis
vibration isolation system. Journal of sound and vibration, 269:913–931, 2004.
LSSP. Low stiffness stewart platform. Technical report, ESA/ESTEC Contract
n16329/02/NL/CP, 2005.
J.E. McInroy, J.F. O’Brien, and G.W. Neat. Precise, fault-tolerant pointing using
a stewart platform. IEEE/ASME Trans. on mechatronics, 4(1):91–95, March
1999.
300:644–661, 2007.
Z.H. Rahman, J.T. Spanos, and R.A. Laskin. Multi-axis vibration isolation, suppression and steering system for space observational applications. In SPIE
International Symposium on Astronomical Telescopes and Instrumentation,
Kona-Hawaii, pages 73–81, March 1998.
J. Spanos, Z. Rahman, and G. Blackwood. A soft 6-axis active vibration isolator. In Proceedings of the IEEE American Control Conference, pages 412–416,
Seattle, Washington, June 1995.
D. Stewart. A platform with six degrees of freedom. Proceedings of the Institution
of Mechanical Engineers, 180(15):371–386, 1965-66.
References
129
D. Thayer, J. Vagners, A. von Flotow, C. Hardham, and K. Scribner. Six-axis
vibration isolation system using soft actuators and multiple sensors (AAS 98064). In Proceeding of the Annual American Astronautical Society (AAS) Rocky
Mountain Guidance & Control Conference, pages 497–506, 1998.
D. Thayer, M. Campbell, J. Vagners, and A. von Flotow. Six-axis vibration
isolation system using soft actuators and multiple sensors. Journal of spacecraft
and rockets, 39(2):206–212, March-April 2002.
130
References
Chapter 8
Conclusions
This thesis investigates the use of shunt circuits as a way to control the vibrations of a mechanical structure and compares this method with “classical” active
control. Damping via piezoelectric transducers and isolation via electromagnetic
(moving-coil) transducers are considered.
In the case of piezoelectric shunt damping, the conclusions are as follows:
• Shunted structures behave as expected: the correlation between numerical
predictions and experimental data is quite good. Approximate formulae
based on the short-circuit and open-circuit natural frequencies of the structure have been developed and validated. It was found that the performances
are mainly governed by two parameters: the piezoelectric electromechanical
coupling factor k 2 and the structural ratio of modal strain energy νi .
• The applications of resistive (R) shunting are limited, as this shunt introduces very little damping in the structure (typically 0.25%-0.5% at most).
Resonant shunting with a resistive-inductive (RL) circuits produces acceptable levels of damping (a few percents), but it requires an electronic
implementation because the optimal value of the inductance is too large
to be implemented with a coil. It is also very sensitive to the tuning of
the electrical resonance on the targeted structural mode: performances can
drop to a large extent if the capacitance of the piezo changes (e.g. because
of a change in temperature) or if the actual natural frequency is different
from the expected one.
• As expected, the negative capacitance shunt enhances the piezoelectric conversion of energy and therefore leads to increased performances of the shunt
circuits. It is however an active system, which must be used with caution
because it can be destabilized if improperly tuned. In particular, non-linear
131
132
8 Conclusions
behavior of the piezoelectric transducer can be an issue. It was also shown
that the effectiveness of the shunt is limited, unless it is tuned quite close
to the stability limit, which is a major issue. Besides, the required levels of
voltage are much higher than those required by RL shunts.
• The attainable levels of damping with active or passive shunts can be one
order of magnitude smaller than those with “classical” active control systems such as Integral Force Feedback (IFF).
The conclusions for vibration isolation with shunted moving-coil transducers, on
the other hand, are as follows:
• In the case of a single-axis isolator, both RL and RLC shunts simultaneously allow good isolation performances (a -40dB/dec attenuation rate)
and reasonable attenuation of the suspension mode. A trade-off between
isolation and damping however applies, because these shunts increase the
corner frequency of the system.
• The equations governing such systems are very similar to those governing
shunted piezoelectric structures. The importance of the transducer constant
Tv2 and that of the coil resistance Rc have been stressed: note that these
coefficients can easily be predicted from a magnetic finite element analysis.
The theory has been validated on a single-axis isolation set-up. A purely
passive implementation was possible because the transducer had a large
Tv2 /Rc coefficient.
• An active shunt circuit is also possible; such a system has been designed and
tested. It was shown, however, that it is less effective than the classical IFF
active control. Besides, no configuration with guaranteed stability could be
found: stability had to be assessed on a case-by-case basis.
• It is possible to build a multi-axis isolator, based on the Stewart platform
architecture, that employs passive shunt circuits. The suspension modes of
the isolator are slightly less damped than what can be achieved with IFF,
but on the other hand the frequency region where the isolation is effective
is larger because the frequency of the first local mode of the legs increases,
thanks to the absence of load cells.
Original aspects of the work
• The extensive analysis of the negative capacitance shunt; the comparison
between the parallel and series implementations and the demonstration
133
that a system “piezo stack and negative capacitance” can be seen as an
equivalent transducer with enhanced electromechanical coupling factor k.
• The stability assessment of the active shunts by means of a Nyquist plot
and a feedback diagram; the use of a modified circuit that enhances the
stability of the parallel shunt. The prediction of the performances from a
single admittance curve.
• The theoretical and experimental comparison between piezoelectric shunt
damping (active and passive) and classical active control with Integral Force
Feedback on a single truss benchmark structure; the experimental verification of the theoretical root loci.
• The theoretical analysis of a single-axis isolator with a moving-coil transducer and various shunt circuits, and the experimental validation of this
analysis.
• The use of a dedicated electronic board that easily emulates the behavior of a large class of admittances; the evaluation of low-pass admittances
(Butterworth filters of order 3 or 4).
• The design of a multi-axis isolator, based on the Stewart Platform architecture, intended to be used with passive RL circuits; the numerical evaluation
of its performances. The design, construction and experimental testing of
a dedicated moving-coil transducer with a given transduction constant Tv2
and minimal coil resistance Rc .
Publications
The work presented in this thesis has led to the following publications:
Book chapter:
B. de Marneffe, A. Preumont. Active Truss Structures. CRC press (submitted)
Journal papers:
• A. Preumont, B. de Marneffe, G. Rodrigues, H. Nasser, A. Deraemaeker.
Dynamics and control in precision mechanics. Submitted to the Revue
Européenne de Mécanique Numérique (REMN).
134
8 Conclusions
• B. de Marneffe, A. Preumont. Vibration control via enhancement of piezoelectric stack actuation: theory and experiment. Submitted to Smart Materials and Structures.
• A. Preumont, B. de Marneffe, S. Krenk. Transmission Zeros in Structural
Control with Collocated MIMO Pairs. Accepted for publication in the AIAA
Journal of Guidance, Control, and Dynamics.
• A. Preumont, B. de Marneffe, A. Deraemaeker, F. Bossens. The damping of
a truss structure with a piezoelectric transducer. Computers and Structures
(in press, corrected proof, March 2007).
• A. Preumont, M. Horodinca, I. Romanescu, B. de Marneffe, M. Avraam, A.
Deraemaeker, F. Bossens, A. Abu Hanieh. A six-axis single-stage active vibration isolator based on Stewart platform. Journal of Sound and Vibration
300 (2007) 644661.
Conference proceedings
• B. de Marneffe, M. Horodinca, A. Preumont. A new semi-active method
for the damping of a piezoelectric structure. Proc. ISMA 2006, Leuven,
Belgium.
• B. de Marneffe, A. Deraemaeker, M. Horodinca, I. Romanescu, A. Preumont.
Active and passive damping of structures with piezoelectric transducers. In
Proc. 7th Nat. Congress on Theoretical and Applied Mechanics, Mons,
Belgium, May 2006.
• A. Preumont, B. de Marneffe, I. Romanescu, M. Horodinca, A. Deraemaeker, and M. Avraam. Zero-gravity experiment of a six-axis single stage
active vibration isolator based on stewart platform. In 16th International
conference on adaptive structures and technologies, Paris, France, October
2005.
• M. Avraam, B. de Marneffe, I. Romanescu, M. Horodinca, A. Deraemaeker,
A. Preumont. A Six Degrees of Freedom Active Isolator Based on Stewart
Platform for Space Applications. 56th International Astronautical Congress
(Paper IAC-05-C2.201), Fukuoka, Japan, Oct. 2005.
• A. Preumont, B. de Marneffe, A. Deraemaeker. Active and passive damping
of piezoelectric structures. In Forum Acusticum 2005, Budapest, Hungary,
Sept 2005
135
• A. Preumont, B. de Marneffe, A. Deraemaeker, F. Bossens. On damping
structures with piezoelectric transducers. II ECCOMAS Thematic Conference on Smart Structures and Materials, Lisbon, Portugal, July 2005.
• B. de Marneffe, M. Avraam, M. Horodinca, I. Romanescu, A. Preumont.
Multi Degree-of-Freedom Active Vibration Isolator for Space Applications.
24th Benelux Meeting on Systems and Control, March 2005, Houffalize,
Belgium.
• A. Abu Anieh, M. Horodinca, B. de Marneffe, I. Romanescu, A. Preumont,
F. Bossens. Actuator Design for a Six-Axis Active Vibration Isolation for
Space Applications. Actuator 2004, Bremen, Germany.
Discussion:
B. de Marneffe. Discussion: “Improved Concept and Model of Eddy current
Damper” (H.A. Sodano, J.-S. Bae, D.J. Inman, W.K. Belvin, 2006, ASME J.
Vib. Acoust., 128), published in the ASME Journal of Vibration and Acoustic
(129), June 2007.
Seminar:
B. de Marneffe. Active damping of large-scale space structures. Workshop on
model reduction and control, Keizerslautern, Germany, May 2007.
136
8 Conclusions
Appendix A
Electrical representation of a
piezoelectric structure
The linear state-space models used in the first part of this thesis (e.g. the feedback
diagrams in Fig. 5.4) do not allow the modelling of the non-linear characteristics of
the electrical components: for example, the influence of the opamps’ bias currents
or that of their saturation level on the overall structure cannot be assessed in this
way. These characteristics are best analyzed in dedicated softwares such as PSpice
(http://www.orcad.com), but these softwares very seldom allow the coupling of
the electric circuit with a model (e.g. FE) of the piezoelectric structure. In
this section we try to solve this issue by creating an electrical representation of
the structure, i.e. an electric circuit which behaves similarly to the piezoelectric
structure seen from the electrodes. Such a circuit can be implemented in PSpice
and allows thus the analysis of the coupling between the structure and the shunt.
Various electrical realizations have already been developed in the literature, but
most of them (such as Park, 2001 or IEEE Std., 1988) concentrate on single-mode
structures or use a modal truncation, which is not convenient for our purposes;
the short developments presented hereafter, by contrast, insist on the modelling
of the quasi-static contribution of the high-frequency modes.
The creation of the electrical representation is done in two steps. First, the
structure is supposed to be at rest, i.e. no external forces are exerted on it; next,
the influence of these forces is added to the model.
137
138
A Electrical representation of a piezoelectric structure
I
I
R1
Cp
R2
L1
L2
C1
C2
Vp
V1
V2
R1
R2
L1
L2
C1
C2
V
V
Cp
(a)
(b)
Figure A.1: Electrical circuit with the same electric behavior as a piezoelectric
two-mode structure; (a) the structure is assumed at rest, (b) an external mechanical force f is taken into account.
A.1
Structure at rest
The admittance of a piezoelectric structure, seen from the electrodes, was analyzed in chapter 4; it is written:
Ã
!
n
2
X
I(s)
ν
ω
i i
= sC 1 − k 2 + k 2
(A.1)
V (s)
s2 + 2ξi ωi s + ωi2
i=1
where, as usual, C is the constant-force piezoelectric capacitance, k 2 is the piezoelectric coupling factor, νi are the fractions of modal strain energy (i = 1, . . . , n),
ωi are the short-circuit natural frequencies of the structure and ξi are the structural damping ratios. If the modal representation is to be truncated after m
modes, a quasi-static correction should be performed; the admittance equation
becomes in this case:
Ã
!
n
m
2
X
X
ν
ω
I(s)
i
i
+ k2
νi
≈ sC 1 − k 2 + k 2
(A.2)
2 + 2ξ ω s + ω 2
V (s)
s
i
i
i
i=1
i=m+1
!
Ãm
2
X
ν
ω
i i
(A.3)
= sCp + sCk 2
2 + 2ξ ω s + ω 2
s
i
i
i
i=1
where Cp is defined as:
Ã
Cp = C
1 − k2 + k2
n
X
i=m+1
!
νi
= Cstatic − Ck 2
m
X
νi
(A.4)
i=1
with Cstatic the capacitance of the piezo under static conditions as defined in
Eq. 4.11 and Eq. 4.12. It is easily verified, by inspection, that the admittance
A.2 Modelling of a perturbation
139
of Eq. A.3 is identical to that of a capacitance Cp connected in parallel to m
series-RLC circuits (Fig. A.1a), if the value of each component Li , Ri and Ci
(i = 1, . . . , m) is given by:
Li =
1
(A.5)
Cωi2 νi k 2
Ri = 2ξi ωi Li =
Ci =
2ξi
Cωi νi k 2
(A.6)
1
= Cνi k 2
Lωi2
(A.7)
This result is illustrated in Fig. A.1a, which represents an electrical circuit totally
equivalent, from an electrical standpoint, to a two-mode piezoelectric structure.
A.2
Modelling of a perturbation
Although the electrical representation described in the previous section (Fig. A.1a)
is sufficient for most purposes, it is sometimes necessary to take into account the
mechanical forces that are exerted on the structure; such a situation occurs, for
example, if the designer wishes to know the maximum voltage and current that
are required of the opamps.
Without loss of generality, we can consider that only one mechanical force f
is exerted on an undamped structure. The constitutive equations of a general
piezoelectric structure were established in chapter 2; they are in this case:
¡
¢
(A.8)
M s2 + K + Ka bbT x = bKa nd33 V + b2 f
I = sC(1 − k 2 )V + snd33 Ka bT x
(A.9)
with M and K the mass and stiffness matrices of the structure (without the
piezo), Ka the short-circuit stiffness of the transducer, n the number of slices in
the stack and d33 a piezoelectric material constant. b and b2 are projection vectors
relating the end displacements of the strut and the position of the external force
f , respectively, to the global coordinate system.
Going into modal coordinates as in chapter 3 and eliminating x from Eq. A.8 and
Eq. A.9, one finds:
I = sC(1 − k 2 )V + sCk 2
n
X
Ka bT Φi ΦT b
i=1
µi (s2 +
i
ωi2 )
V + snd33
n
X
Ka bT Φi ΦT b2
i
i=1
µi (s2 + ωi2 )
f (A.10)
Similarly to the coefficients νi (Eq. 2.33), one can define a set of coefficients νi0 :
νi0 ,
Ka bT Φi ΦTi b2
Ka (ΦTi b)(ΦTi b2 )
=
µi ωi2
µi ωi2
(A.11)
140
References
that mixes the projection vector b of the transducer with the projection vector
b2 of the external force f . Eq. A.10 becomes:
µ
¶
n
X
νi ωi2
nd33 νi0
2
2
I = sC(1 − k )V + sCk
V +
f
(A.12)
Ck 2 νi
s2 + ωi2
i=1
As expected, Eq. A.12 reduces to Eq. A.1 when f = 0. In the more general case,
one sees that f can be modelled as a set of additional voltages Vi (i = 1, . . . , n)
in each RLC branch as illustrated in Fig. A.1b; each Vi is related to f by:
Vi =
nd33 νi0
1
(ΦTi b2 )
f
=
f
Ck 2 νi
nd33 Ka (ΦTi b)
(A.13)
where the definition of k 2 (Eq. 2.17) has been used. Once again, if the modal
representation is to be truncated after m modes, it is best to take into account the
quasi-static contribution of the discarded modes. This can be done by introducing
a voltage Vp in series with the capacitance Cp (Fig. A.1b); indeed, Eq. A.12
becomes in this case:
µ
¶
m
X
νi ωi2
nd33 νi0
2
I ≈ sCp (V + Vp ) + sCk
V +
f
(A.14)
Ck 2 νi
s2 + ωi2
i=1
where Eq. A.4 has been used and Vp is given by:
n
nd33 X 0
Vp =
νi f
Cp
i=m+1
!
Ã
m
X
1
Qstatic − nd33
νi0 f
=
Cp
(A.15)
(A.16)
i=1
Qstatic (in Coulomb/Newton) is defined as the electric charge appearing on the
short-circuited electrodes if a unitary force f is applied under static conditions.
Qstatic is most easily evaluated with a FE model of the structure; from Eq. A.8
and Eq. A.9, it is also given by:
¡
¢−1
b2
(A.17)
Qstatic = nd33 Ka bT K + Ka bbT
A.3
References
C. H. Park. On the circuit model of piezoceramics. Journal of Intelligent Material
Systems and Structures, 12:515–522, July 2001.
General Bibliography
S. Alessandroni, U. Andreaus, F. dell’Isola, and M. Porfiri. A passive electric
controller for multimodal vibrations of thin plates. Computers and Structures,
83:1236–1250, 2005.
1341, Nov. 1990.
A. Antoniou. Realisation of gyrators using operational amplifiers, and their use
in RC-active-network synthesis. Proc. IEE., 116(11):1838–1850, Nov. 1969.
T. Asami, O. Nishihara, and A.M. Baz. Analytical solutions to H∞ and H2 optimization of dynamic vibration absorbers attached to damped linear systems.
ASME J. of Vibration and Acoustics, 124:284–295, April 2002.
J.N. Aubrun. Theory of the control of structures by low-authority controllers. J.
Guidance and Control, 3(5):444–451, Sept.-oct. 1980.
M. Avraam, B. de Marneffe, I. Romanescu, M. Horodinca, A. Deraemaeker, and
A. Preumont. A six degrees of freedom active isolator based on stewart platform
for space applications. In 56th International Astronautical Congress (Paper
IAC-05-C2.201), Fukuoka, Japan, Oct. 2005.
M.J. Balas. Direct velocity feedback control of large space structures. AIAA
Journal of Guidance and Control, 2(3):252–253, 1979.
S. Behrens, A.J. Fleming, and S.O.R. Moheimani. A broadband controller for
shunt piezoelectric damping of structural vibration. Smart Materials and Structures, 12:18–28, 2003.
141
142
S. Behrens, A.J. Fleming, and S.O.R. Moheimani. Passive vibration control via
electromagnetic shunt damping. IEEE/ASME transactions on mechatronics,
10(1):118–122, Feb. 2005.
A. Benjeddou, M.A. Trindade, and R. Ohayon. A unified beam finite element
model for extension and shear piezoelectric actuation mechanisms. Journal of
Intelligent Material Systems and Structures, 8:1012–1025, Dec. 1997.
937, 2006.
I. Bonev. The true origins of parallel robots.
http://www.parallemic.org/Reviews/Review007.html, 2003.
F. Bossens. Amortissement actif des structures câblées: de la théorie à
l’implémentation. PhD thesis, Université Libre de Bruxelles, 2001.
P. W. Bousquet, P. Guay, and F. Mercier. CASTOR active damping experiment, preliminary flight results. Journal of Intelligent Material Systems and
Structures, 8(9):792–800, 1997.
1996.
A.J. Bronowicki, N.S. Abhyankar, and S.F. Griffin. Active vibration control
of large optical space structures. Smart Materials and Structures, 8:740–752,
1999.
S.E. Burke and J.E. Hubbard. Active vibration control of a simply supported
beam using a spatially distributed actuator. IEEE control system magazine,
pages 25–30, Aug. 1987.
W. G. Cady. Piezoelectricity: An Introduction to the Theory and Applications of
Electromechanical Phenomena in Crystals. Mc Graw-Hill, New-York, London,
1946.
G. Caruso. A critical analysis of electric shunt circuits employed in piezoelectric
passive vibration damping. Smart Materials and Structures, 10:1059–1068,
2001.
paper 89-1327 CP, 1989.
143
G.S. Chen, R.J. Bruno, and M. Salama. Optimal placement of active/passive
members in truss structures using simulated annealing. AIAA Journal, 29(8):
1327–1334, Aug. 1991.
W.W. Clark. Vibration control with state-switched piezoelectric materials. Journal of Intelligent Material Systems and Structures, 11:263–271, April 2000.
R.H. Comstock. Charge control of piezoelectric actuators to reduce hysteresis
effects. Us patent 4,263,527, 1981.
E.F. Crawley and J. de Luis. Use of piezoelectric actuators as elements of intelligent structures. AIAA Journal, 25(10):1373–1385, Oct. 1987.
M. Date, M. Kutani, and S. Sakai. Electrically controlled elasticity utilizing
piezoelectric coupling. J. Applied Physics, 87(2):863–868, Jan. 2000.
C.L. Davis and G.A. Lesieutre. A modal strain energy approach to the prediction
of resistively shunted piezoceramic damping. Journal of Sound and Vibration,
184(1):129–139, 1995.
B. de Marneffe and A. Deraemaeker. State-space models of structures equipped
with MFCs (macro-fibres composites) in Matlab/Simulink. InMAR technical
report D173 (WA2.1), ULB, 2006.
B. de Marneffe, A. Abu Hanieh, M. Avraam, A. Deraemaeker, M. Horodinca,
I. Romanescu, and A. Preumont. A novel design of stewart platform for active
vibration isolation. 38th ESA parabolic flight campaign final report (Prodex90147), Oct. 2004.
CRC Press, 1999.
J.P. Den Hartog. Mechanical Vibrations. McGraw-Hill, New-York, 4th edition,
1956.
C. Dörlemann, P. Muß, M. Schugt, and R. Uhlenbrock. New high speed current
controled amplifier for pzt multilayer stack actuators. In Actuator02, Bremen,
Germany, 2002.
D.L. Edberg, A.S. Bicos, C.M. Fuller, J.J. Tracy, and J.S. Fechter. Theoretical
and experimental studies of a truss incorporationg active members. J. of Intell.
Mater. Syst. and Struct., 3:333–347, April 1992.
R.H. Edwards and R.H. Miyakawa. Large structure damping tasks report. Technical Report 4132.22/1408, Hughes Aircraft Co., 1980.
144
C. Ehmann, U. Schönhoff, and R. Nordmann. Robust controller synthesis vs.
integral force feedback with collocation for active damping of flexible structures.
In Proc. ISMA 2002, Leuven, Belgium, 2002.
J.L. Fanson, G.H. Blackwood, and C.C. Chu. Active-member control of precision
structures. In SDM Conference, pages 1480–1494. AIAA paper 89-1329 CP,
1989.
Optics, 18(5):690–697, March 1979a.
R.L. Forward. Electromechanical transducer-coupled mechanical structure with
negative capacitance compensation circuit. Us patent 4,158,787, 1979b.
R.L. Forward. Electronic damping of orthogonal bending modes in a cylindrical
mast - experimental. J. Spacecraft, 18(1):11–17, Jan.-Feb. 1981.
C.R. Fuller, S.J. Elliott, and P.A. Nelson. Active Control of Vibration. Academic
Press, 1996.
Z.J. Geng and L.S. Haynes. Six degree-of-freedom active vibration control using
the stewart platforms. IEEE Transactions on control systems technology, 2(1):
45–53, March 1994.
V.E. Gough and S.G. Whitehall. Universal tyre testing machine. In Proc. Ninth
International Technical Congress F.I.S.I.T.A., 117, 1962.
D. Guyomar and C. Richard. Non-linear and hysteretic processing of piezoelement: Application to vibration control, wave control and energy harvesting.
International Journal of Applied Electromagnetics and Mechanics, 21:193–207,
2005.
S. Hanagaud, M.W. Obal, and A.J. Calise. Optimal vibration control by the
use of piezoceramic sensors and actuators. Journal of Guidance, Control and
Dynamics, 15(5):1199–1206, Sept.-Oct. 1992.
145
G.S. Hauge and M.E. Campbell. Sensors and control of a space-based six-axis
vibration isolation system. Journal of sound and vibration, 269:913–931, 2004.
M.H. Holnusen and K.A. Cunefare. Damping effects on the state-switched absorber used for vibration suppression. Journal of Intelligent Material Systems
and Structures, 14:551–561, Sept. 2003.
H. Janocha. Adaptronics and Smart Structures: Basics, Materials, Design, and
Applications. Springer, 1999. (Editor).
D.C. Karnopp and A.K. Trikha. Comparative study of optimization techniques
for shock and vibration isolation. Trans. ASME Journal of Engineering for
Industry, series B, 91(4):1128–1132, 1969.
J.S. Kim, K.W. Wang, and E.C. Smith. High-authority piezoelectric actuation
system synthesis through mechanical resonance and electrical tailoring. J. of
Intelligent Material Systems and Structures, 16:21–31, Jan. 2005.
G.A. Lesieutre, G.K. Ottman, and H.F. Hofmann. Damping as a result of piezoelectric energy harvesting. Journal of Sound and Vibration, 269:991–1001,
2004.
N Loix, A. Conde Reis, P. Brazzale, J. Detteman, and A. Preumont. CFIE:
In-orbit active damping experiment using strain actuators. In Space Microdynamics and Accurate Control Symposium, Toulouse, France, May 1997.
LSSP. Low stiffness stewart platform. Technical report, ESA/ESTEC Contract
n16329/02/NL/CP, 2005.
L.Y. Lu, S. Utku, and B.K. Wada. On the placement of active members in
adaptive truss structures for vibration control. Smart Materials and Structures,
1:8–23, 1992.
J.A. Main, E. Garcia, and D.V. Newton. Precision position control of piezoelectric
actuators using charge feedback. J. of Guidance, Control and Dynamics, 18
(5):1068–1073, Sept.-Oct. 1995.
C. Maurini. Piezoelectric Composites for Distributed Passive Electric Control:
Beam Modelling, Modal Analysis, and Experimental Implementation. PhD
146
thesis, Université Pierre et Marie Curie (Paris) and Università di Roma “La
Sapienza”, 2005.
C. Maurini, F. dell’Isola, and D. Del Vescovo. Comparison of piezoelectronic
networks acting as distributed vibration absorbers. Mechanical Systems and
Signal Processing, 18:12431271, 2004.
J.E. McInroy, J.F. O’Brien, and G.W. Neat. Precise, fault-tolerant pointing using
a stewart platform. IEEE/ASME Trans. on mechatronics, 4(1):91–95, March
1999.
M. Neubauer, R. Oleskiewicz, K. Popp, and T. Krzyzynski. Optimization of
damping and absorbing performance of shunted piezo elements utilizing negative capacitance. Journal of Sound and Vibration, 298:84–107, 2006.
C.V. Newcomb and I. Flinn. Improving the linearity of piezoelectric ceramic
actuators. Electronics Letters, 18(11):442–443, 1982.
D. Niederberger. Smart Damping Materials Using Shunt Control. PhD thesis,
Swiss federal institute of technology (ETH) Zurich, 2005.
D. Niederberger, A. Fleming, S.O.R. Moheimani, and M. Morari. Adaptive multimode resonant piezoelectric shunt damping. Smart Materials and Structures,
13:1025–1035, 2004.
T.W. Nye, A.J. Bronowicki, R.A. Manning, and S.S. Simonian. Applications of
robust damping treatments to advanced spacecraft structures. Advances in the
Astronautical Sciences, 92:531–543, Feb. 1996.
T.W. Nye, R.A. Manning, and K. Qassim. Performance of active vibration control
technology: The ACTEX flight experiments. Smart Materials and Structures,
8:767–780, 1999.
S.L. Padula and R.K Kincaid. Optimization strategies for sensor and actuator
placement. Technical report TM-1999-209126, NASA Langley Research Center,
1999.
C. H. Park. On the circuit model of piezoceramics. Journal of Intelligent Material
Systems and Structures, 12:515–522, July 2001.
C.H. Park and A. Baz. Vibration control of beams with negative capacitive
shunting of interdigitated electrode piezoceramics. Journal of Vibration and
Control, 11:331–346, 2005.
147
C.H. Park and D.J. Inman. Enhanced piezoelectric shunt design. Shock and
Vibration, 10:127–133, 2003.
C. Paulitsch, P. Gardonio, and S.J. Elliott. Active vibration damping using an
inertial, electrodynamic actuator. ASME Journal of Vibration and Acoustics,
129:39–47, Feb. 2007.
C.Y. Peng, M. Levine, L. Shido, and R. Leland. Experimental observations
on material damping at cryogenic temperatures. In SPIE 49th International
Symposium on Optical Science and Technology, Denver, Colorado, August 2-6,
2004., Aug. 2004. http://hdl.handle.net/2014/40006.
Philbrick Researches Inc. Application manual for computing amplifiers for modelling, measuring, manipulating & much else. Technical report, Nimrod Press,
Boston, 1965.
M. Porfiri. Performances of Passive Electric Networks and Piezoelectric Transducers for Beam Vibration Control. PhD thesis, Università di Roma “La
Sapienza” and Université de Toulon et du Var, 2005.
2002. 2nd edition.
A. Preumont, A. François, F. Bossens, and A Abu-Hanieh. Force feedback versus acceleration feedback in active vibration isolation. Journal of Sound and
Vibration, 257(4):605–613, 2002.
A. Preumont, B. de Marneffe, A. Deraemaeker, and F. Bossens. The damping of
a truss structure with a piezoelectric transducer. Computers and Structures,
March 2007a. in press, corrected proof.
300:644–661, 2007b.
Z.H. Rahman, J.T. Spanos, and R.A. Laskin. Multi-axis vibration isolation, suppression and steering system for space observational applications. In SPIE
148
International Symposium on Astronomical Telescopes and Instrumentation,
Kona-Hawaii, pages 73–81, March 1998.
S.S. Rao, T.S. Pan, and V.B. Venkayya. Optimal placement of actuators in
actively controlled structures using genetic algorithms. AIAA Journal, 29(6):
942–943, June 1991.
K.H. Rew and I. Lee. Adaptive shunting for vibration control of frequencyvarying structures. Journal of Guidance, Control and Dynamics, 24(6):1223–
1224, Nov.-Dec. 2001.
J. Spanos, Z. Rahman, and G. Blackwood. A soft 6-axis active vibration isolator. In Proceedings of the IEEE American Control Conference, pages 412–416,
Seattle, Washington, June 1995.
D. Stewart. A platform with six degrees of freedom. Proceedings of the Institution
of Mechanical Engineers, 180(15):371–386, 1965-66.
C.J. Swigert and R.L. Forward. Electronic damping of orthogonal bending modes
in a cylindrical mast - theory. J. Spacecraft, 18(1):5–10, Jan.-Feb. 1981.
10:794–806, 2001.
D. Thayer, J. Vagners, A. von Flotow, C. Hardham, and K. Scribner. Six-axis
vibration isolation system using soft actuators and multiple sensors (AAS 98064). In Proceeding of the Annual American Astronautical Society (AAS) Rocky
Mountain Guidance & Control Conference, pages 497–506, 1998.
D. Thayer, M. Campbell, J. Vagners, and A. von Flotow. Six-axis vibration
isolation system using soft actuators and multiple sensors. Journal of spacecraft
and rockets, 39(2):206–212, March-April 2002.
B.K. Wada. Summary of precision actuators for space application. Technical
report, Jet Propulsion Laboratory (JPL), 1993. http://citeseer.ist.psu.edu
/344213.html.
S.Y. Wu. Broadband piezoelectric shunts for structural vibration control. Us
patent 6,075,309, 2000.
S.Y. Wu. Method for multiple mode piezoelectric shunting with single PZT
transducer for vibration control. Journal of Intelligent Material Systems and
Structures, 9:991–998, Dec. 1998.
149
H. Yu and K.W. Wang. Piezoelectric networks for vibration suppression of mistuned baled disks. ASME Journal of Vibration and Accoustics, 129:559–566,
Oct 2007.
H. Yu, K.W. Wang, and J. Zhang. Piezoelectric networking with enhanced
electromechanical coupling for vibration delocalization of mistuned periodic
structures-theory and experiment. Journal of Sound and Vibration, 295:246–
265, 2006.

Active and Passive Vibration Isolation and Damping via Shunted

Transcription

Documents pareils

Impedance Box

PDF

PJ Stock 2009 - Patrick Jefferson

ITHOME Sanctuary of Artemis Limnatis

2013 cb1000r specifications

SARONIC HARBOURS ARCHAEOLOGICAL RESEARCH PROJECT

Osteology Venedig Mai 98_Poster Diffraktometrie HA_TCP

VibroSens 401 en - SCHMIDT Technology GmbH

Poster Rettungsdienst Israel 2010 PP 2003 KORREKTUR

Kit Instructions