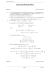Bac blanc Corrigé 1 EXERCICE 1 1. Réponse c) . On vérifie en effet

Bac blanc
Corrigé
EXERCICE 1
1. Réponse c) . On vérifie en effet :
2 (3 − i) + (3 − i) = 2 (3 + i) + 3 − i = 6 + 2i + 3 − i = 9 + i
2. Réponse b) .
√
Écrivons Z = −1 + i 3 sous forme trigonométrique.
q
√
√
Le module est |Z| = (−1)2 + ( 3)2 = 4 = 2

−1

cos φ =
√2 ⇐⇒ φ = 2π + k · 2π
k∈Z
Si φ est un argument de Z, on vérifie

3
 sin φ = 3
2
Z
2π
D’après le cours : arg
= arg(Z) − arg(z) =
−θ
z
3
3. Réponse c) .
On sait que AM = |zM − zA | = |z − 1| et BM = |zM − zB | = |z − (−i)| = |z + i|
L’ensemble cherché est donc l’ensemble des points M qui vérifient M A = M B, c’est-à-dire la
médiatrice du segment [AB]
4. Réponse b) .
z+i
Calculons la partie réelle et la partie imaginaire de Z =
en fonction de x et y :
z+1
(x + iy) + i
x + i(y + 1)
x + i(y + 1) (x + 1) − iy
Z=
=
=
·
(x + iy) + 1
(x + 1) + iy
(x + 1) + iy (x + 1) − iy
=
[x(x + 1) + (y + 1)] + i [(y + 1)(x + 1) − xy]
(x + 1)2 + y 2
x2 + y 2 + x + y
x+y+1
+
i
(x + 1)2 + y 2
(x + 1)2 + y 2
Par conséquent, si Z est un imaginaire pur, sa partie réelle doit s’annuler et les coordonnées
du point M doivent vérifier :
2 2
1
1
1
2
2
x + y + x + y ⇐⇒ x +
+ y+
=
2
2
2
5. Réponse c) .
Pour tout z 6= 3, cette équation est équivalente à :
z − 8 = z(z − 3) ⇐⇒ z 2 − 4z + 8 = 0
On vérifie ensuite que le discriminant est ∆ = (−4)2 − 4 × 8 = −16 = (4i)2
L’équation a donc deux solutions complexes conjuguées
4 − 4i
z1 =
= 2 − 2i
et
z2 = z1 = 2 + 2i
2
=
1
Bac blanc
Corrigé
EXERCICE 2
1. On a directement P (N1 ) = 0, 7 et PN1 (R2 ) = 0, 1 par lecture du texte.
On en déduit P (N1 ∩ R2 ) = P (N1 ) PN1 (R2 ) = 0, 07 .
2.
V
0,2
0,1
0,8
N
0,2
R
0,2
V
R
0,7
N
0,1
R
0,7
N
3. On peut écrire E = R1 ∩ R2 et donc p(E) = p(R1 ) pR1 (R2 ) = 0,02
L’événement F est la réunion disjointe des événements R1 ∩ N2 et N1 ∩ R2 :
p(F ) = p(R1 ∩ N2 ) + p(N1 ∩ R2 )
= p(R1 ) pR1 (N2 ) + p(N1 ) pN1 (R2 )
= 0, 1 × 0, 8 + 0, 7 × 0, 1 = 0,15
4. a) On applique la formule des probabilités totales :
p(R2 ) = p(R1 ∩ R2 ) + p(N1 ∩ R2 )
= P (R1 ) PR1 (R2 ) + P (N1 ) PN1 (R2 )
= 0, 1 × 0, 2 + 0, 7 × 0, 1
= 0, 02 + 0, 07 = 0,09
p(R2 ∩ N1 )
7
b) Par définition pR2 (N1 ) =
=
p(R2 )
9
5. a) Le gain algébrique du joueur est la différence entre le gain et la somme qu’il a misée.
Les valeurs prises par la variable aléatoire X sont donc 9 , 1 et -1 .
D’après l’étude précédente, p(X = 9) = p(E) = 0, 02 et p(X = 1) = p(F ) = 0, 15. On en
déduit p(X = −1) = 1 − p(X = 9) − p(X = 1) = 0, 83
On peut résumer les résultats dans un tableau :
xi
9
1
-1
pi
0,02
0,15
0,83
b) Par définition E(X) = 9 × 0, 02 + 1 × 0, 15 − 1 × 0, 83 = −0, 5
Le jeu est défavorable au joueur puisqu’il perd en moyenne 0,5¤ à chaque partie.
6. a) On répète la même expérience en supposant les résultats indépendants.
Si on appelle succès le fait de lancer la roue B au second lancer, la variable aléatoire Y qui
est égale au nombre de succès suit une loi binomiale de paramètres n et p(R1 ) = 0, 1 .
On veut calculer p(Y ≥ 1) . On sait que l’événement contraire est (Y = 0) et que sa
probabilité est
n
p(Y = 0) =
0, 10 0, 9n = 0, 9n
0
2
Bac blanc
Corrigé
On en déduit pn = 1 − 0, 9n .
b) Sachant −1 < 0, 9 < 1 on peut écrire lim 0, 9n = 0 et par somme lim pn = 1
La suite (pn ) est donc convergente.
c) On résout :
pn ≥ 0, 99 ⇐⇒ 1 − 0, 9n ≥ 0, 9
⇐⇒ 0, 1 ≥ 0, 9n
⇐⇒ ln 0, 1 ≥ n ln 0, 9
En divisant les deux membres par ln 0, 9 < 0, on obtient n ≥
La plus petite valeur de n telle que pn ≥ 0, 99 est donc 22 .
3
ln 0, 1
≈ 21, 85
ln 0, 9
Bac blanc
Corrigé
EXERCICE 3
1. D’après le cours lim x ln x = 0 . On en déduit par somme lim g(x) = −1
x→0
x→0
Sachant lim ln x = +∞, on obtient par produit puis par somme lim g(x) = +∞
x→+∞
x→+∞
1
2. Posons u(x) = x et u0 (x) = 1 puis v(x) = ln x et v 0 (x) =
x
On obtient en appliquant la formule de dérivation d’un produit :
1
g 0 (x) = 1 × ln x + x × = ln x + 1
x
On étudie maintenant 
le signe de cette dérivée :
0
−1
g (x) = 0 ⇐⇒ ln x = −1 ⇐⇒ x = e
g 0 (x) > 0 ⇐⇒ ln x > −1 ⇐⇒ x > e−1
 0
g (x) < 0 ⇐⇒ ln x < −1 ⇐⇒ x < e−1
On en déduit le tableau de variations de g
x
e−1
0
0
−
g (x)
0
+∞
+
+∞
−1
−1 − e−1
g(x)
3. La fonction g est continue et strictement décroissante sur 0 ; e−1 : l’intervalle image est donc
−1 − e−1 ; −1
Cet intervalle ne contenant pas 0, l’équation g(x) = 0 n’a pas de solution dans 0 ; e−1
La fonction g est continue et strictement croissante sur e−1 ; +∞ : l’intervalle image est donc
−1 − e−1 ; +∞
Cet intervalle contenant 0, l’équation g(x) = 0 a une solution α et une seule dans e−1 ; +∞ .
On vérifie enfin g(1, 7) ≈ −0, 1 < 0 et g(1, 8) ≈ 0, 06 > 0, ce qui implique 1, 7 < α < 1, 8
4. On a montré dans la question précédente que si x ∈ −1 − e−1 ; −1 , alors g(x) < 0
−1
Par ailleurs, puisque g est 
strictement croissante sur e ; +∞ , on peut écrire :
e−1 < x < α =⇒ g(x) < g(α) = 0
x=α
=⇒ g(x) = g(α) = 0

α<x
=⇒ 0 = g(α) < g(x)
1
5. L’abscisse du point d’intersection des courbes C1 et C2 est solution de l’équation = ln x
x
Puisque x > 0, cett équation est équivalente à 1 = x ln x donc à g(x) = 0
D’après l’étude précédente, il y a un point d’intersection A et un seul d’abscisse α et d’ordon1
née = ln α
α
Partie B
1. D’après le cours lim e−x = e0 = 1 et lim ln x = −∞ .
x→0
x→0
On en déduit par produit puis par somme lim f (x) = −∞
x→0
La courbe de f admet pour asymptote verticale la droite d’équation x = 0 (ou encore l’axe
des ordonnées)
ln x
x
ln x
On vérifie de façon immédiate que pour x > 0 :
× x − 1 = x − 1 = f (x)
x
e
e
4
Bac blanc
Corrigé
Par application du cours (théorèmes sur la croissance comparée)
ln x
x
lim
=0
et
lim x = 0
x→+∞ x
x→+∞ e
On en déduit lim f (x) = −1
x→+∞
La courbe de f admet pour asymptote horizontale la droite d’équation y = −1
1
2. Posons u(x) = e−x et u0 (x) = −e−x puis v(x) = ln x et v 0 (x) =
x
On obtient en appliquant la formule de dérivation d’un produit :
1
−e−x x ln x + e−x
−e−x g(x)
f 0 (x) = −e−x × ln x + e−x × =
=
x
x
x
Puisque l’exponentielle est strictement positive et puisque x > 0, cette dérivée est du signe de
−g(x) . L’étude ayant été faite dans la partie A, on peut reporter les résultats et construire
le tableau de variations de f :
x 0
α
+∞
f 0 (x)
0
+
−
f (α)
f (x)
−∞
−1
1
= ln α. Ceci implique :
α
1
f (α) = e−α ln α − 1 = α − 1
αe
3. On a vu dans la partie A que
4. Figure
5. Puisque les deux points ont la même abscisse, la distance entre ces points est :
1
eα − 1
1
AB = yA − yB = − α + 1 = 1 +
α αe
α
On a montré que α > 1, 7, ce qui implique α > 0 et donc eα > 1
eα − 1
> 0 et donc finalement AB > 1
On en déduit AB − 1 =
α
5
Bac blanc
Corrigé
EXERCICE 4
1 1
1. On vérifie d’abord que s0 = + = 1
2 2
Supposons que pour un certain entier n on ait vérifié sn = 1 . Alors
an bn 2an bn
sn+1 = an+1 + bn+1 =
+
+
+
= an + bn = sn = 1
3
2
3
2
On a donc pour tout n : sn = 1
an bn
2. On sait que pour tout n : an+1 =
+
3
2
En remplaçant bn par 1 − an , on obtient :
an 1 − an
−an 1
an+1 =
+
=
+
3
2
6
2
3. Tableau numérique :
n
0
1
2
3
4
valeur affichée de a 0,417
0,431 0,428
0,429 0,429
La suite paraît converger vers un réel approximativement égal à 0,429 .
4. a) On calcule un+1 en fonction de un :
3
7
−an 1 3
+ −
6
2 7
−an
1
+
6
14
−1
6
an −
6
14
−1
3
an −
6
7
−1
un
6
un+1 = an+1 −
=
=
=
=
=
La suite (un ) est donc géométrique.
1 3
1
−1
b) Le premier terme est u0 = − =
et la raison est q =
2 7
14
6
n
1
−1
c) On sait que pour tout entier n, on a : un = u0 q , ce qui implique un =
·
14
6
n
−1
−1
< 1, on obtient lim
= 0 et on en déduit (par produit) lim un = 0
5. Sachant −1 <
6
6
3
3
Enfin an = un + entraîne lim an = ` =
7
7
n
6
Bac blanc
Corrigé
ANNEXE (EXERCICE 1)
C2
C1
A
B
C
1
et C2 : y = ln x
x
Unités : 1cm en abscisse et 2cm en ordonnée .
Représentation des courbes
C1 : y =
7