LES GAZ, PARTIE C :

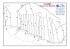
Chapitre V : Les gaz, Partie C
page 1/9
LES GAZ, PARTIE C :
Le modèle de Van der Waals
Nous cherchons une nouvelle équation d’état des gaz car l’expérience montre que le comportement
des gaz réels s’écarte de celui des gaz parfaits aux fortes pressions. Van der Waals1 a proposé une
équation en 1873. Cela, avec d’autres travaux, lui a valu le prix Nobel 1910.
Nous allons décrire comment obtenir l’équation d’état de Van der Waals à partir de considérations
théoriques, en nous fondant sur les limitations du modèle du gaz parfait. En effet, d’une part, les
molécules d’un gaz réel ne sont pas ponctuelles et, d’autre part, elles interagissent entre elles,
contrairement aux hypothèses faites pour définir le gaz parfait.
Ensuite nous visualiserons l’équation de Van der Waals à l’aide de diagrammes.
A. Vers l’équation d’état de Van der Waals
Nous allons d’abord modifier l’équation d’état des gaz parfait en tenant compte du caractère non
ponctuel des molécules.
1. Caractère non ponctuel des molécules
a) Volume propre des molécules
Les molécules d’un gaz réel ne sont pas ponctuelles : elles occupent un certain volume, appelé
volume propre des molécules. Par exemple, en première approximation, on peut assimiler la
molécule d’hélium He à une sphère de rayon r = 1,33.10-10 m. Le volume propre d’une molécule
est alors :
v1 = (4/3)  r3 ≈ (4/3)  (1,33.10-10)3 m3 ≈ 0,985.10-29 m3.
A l’échelle macroscopique, nous considérons le volume propre molaire :
vm = NA v1 ≈ 6,02.1023 (4/3)  (1,33.10-10)3 m3.mol-1
vm ≈ 5,93.10-6 m3.mol-1 ≈ 6 cm3.mol-1.
Dans les conditions normales de température et de pression, le volume molaire des gaz vaut
environ 22400 cm3.mol-1. Le volume propre molaire est alors petit devant le volume molaire du
gaz.
b) Le covolume
Chaque molécule occupe donc un volume qui n’est plus disponible pour les autres. Celles-ci ne
sont donc pas susceptibles de se déplacer dans le volume V du récipient mais dans un volume
1
Voir une courte biographie de Johannes Diderik Van der Waals dans le complément III.1
Chapitre V : Les gaz, Partie C
page 2/9
inférieur que nous noterons V – B. La grandeur B, positive, est appelé covolume et a la dimension
d’un volume (unité légale le m3).
Le covolume est proportionnel au nombre de molécules donc à la quantité de matière n ce que
nous écrivons B = n b. La grandeur b est le covolume molaire et a la dimension d’un volume
molaire (unité légale, le m3.mol-1). Voici quelques mesures de covolumes molaires. Remarquons
qu’ils sont tous du même ordre de grandeur, quelques dizaines de cm3.mol-1.
Hélium
23,7
Dihydrogène
26,6
Dioxygène
31,8
Diazote
39,1
CO2
42,7
cm3.mol-1
Le covolume n’est en fait pas égal au volume propre des molécules. Mais il est du même ordre de
grandeur. Des considérations théoriques quantitatives conduisent à la relation b = 4 vm. (Voir
complément V.1.) Dans les conditions normales de température et de pression, le covolume est
donc faible devant le volume V du gaz.
Nous pouvons vérifier la relation b = 4 vm dans le cas de l’hélium :
4 vm ≈ 4. 5,93.10-6 m3.mol-1 ≈ 2,37.10-5 m3.mol-1 ≈ b
c) Equation partiellement modifiée
Nous transformons alors l’équation d’état des gaz parfaits en une équation d’état de gaz à
molécules non ponctuelles (mais n’interagissant pas entre elles) en remplaçant V par V - B :
p(V  B)  nRT
Nous pouvons aussi écrire pour 1 mole de gaz, en divisant par n et en notant Vm est le volume
molaire :
V B 
p    R T
n n
p(Vm  b)  RT
Nous allons maintenant tenir compte des interactions entre molécules dans un gaz réel.
2. Existence des interactions entre molécules
a) Pression interne
Considérons une molécule au sein du gaz, loin de toute paroi du récipient. A cause des forces de
Van der Waals, elle est attirée de toute part par les autres molécules du gaz. Mais la situation est
symétrique, donc ces attractions se compensent entre elles. Voir figure 1.
Considérons maintenant une molécule proche d’une paroi. Les attractions de Van der Waals
qu’elle subit l’attirent vers l’intérieur du récipient. La pression exercée par le gaz réel sur la
paroi est donc inférieure à celle qu’exercerait un gaz parfait. La différence entre ces deux
pressions est appelée pression interne pi.
Chapitre V : Les gaz, Partie C
page 3/9
paroi
Figure 1 : Forces de Van der Waals subies par une molécule loin de toutes parois et proche d’une paroi
Des considérations théoriques quantitatives montrent que la pression interne est
proportionnelle au carré de la quantité de matière n et inversement proportionnelle au carré du
volume V. En notant a le coefficient de proportionnalité, appelé coefficient de pression interne,
nous écrivons donc :
pi  a
Hélium
3,44
n2
a
 2
2
V
Vm
Dihydrogène
24,7
Dioxygène
138
Diazote
139
CO2
364
mJ.m3.mol-2
Ces valeurs appellent quelques commentaires.
b) Commentaires
i. Le coefficient de pression interne dépend nettement de la nature du gaz, il varie de quelques
mJ.m3.mol-2 à quelques centaines.
ii. Vérifions l’unité légale du coefficient de pression interne. Rappelons que pV a la dimension
d’une énergie et s’exprime donc en joules (voir chapitre III § D.3.a). La dimension du volume
molaire est le m3.mol-1. Celle du coefficient a est telle que le terme a/Vm2, qui représente une
pression, s’exprime en pascals :
u (a)  Pa.m6 .mol-2  Pa.m3 .m3 .mol-2
u (a)  J.m3 .mol-2
iii. Calculons la pression interne dans une mole d’hélium prise dans les conditions normales de
température et de pression. Dans ces conditions, le volume molaire vaut 22,4.10-3 m-3.mol-1 et la
pression interne :
pi0(He) ≈ 3,44.10-3. (1/ 22,4.10-3)2 Pa ≈ 6,86 Pa.
Dans le cas du diazote et du dioxyde de carbone, nous obtenons successivement :
pi0(N2) ≈ 139.10-3. (1/ 22,4.10-3)2 Pa ≈ 277 Pa.
Chapitre V : Les gaz, Partie C
page 4/9
pi0(CO2) ≈ 364.10-3. (1/ 22,4.10-3)2 Pa ≈ 725 Pa.
Il faut comparer ces résultats aux pressions usuelles des gaz, par exemple à la pression normale
P0 = 1,013.105 Pa. La pression interne est donc usuellement faible devant la pression p du gaz.
c) Equation partiellement modifiée
Le terme (p+pi) représente la pression exercée par le gaz parfait, la pression p exercée par le gaz
réel lui est effectivement inférieure.
Nous transformons alors l’équation d’état des gaz parfaits en une équation d’état de gaz (à
molécules ponctuelles) interagissant entre elles en remplaçant p par p+pi :

n2 
p

a

V  n R T
V2 

Puis pour 1 mole de gaz, en divisant par n,

n2  V
 pa 2   RT
V n


a 
 p  2  Vm  R T
Vm 

3. Equation d’état de Van der Waals
a) Son expression
En tenant compte à la fois du covolume et de la pression interne nous écrivons l’équation d’état
de Van der Waals pour n moles de gaz :

n2 
p

a

 (V  nb)  n R T
V2 

Ou pour 1 mole de gaz :

a 
 p  2  (Vm  b)  R T
Vm 

b) Ses intérêts
i. L’étude des gaz réels et de cette équation montre qu’un gaz de Van der Waals est plus proche
d’un gaz réel qu’un gaz parfait.
La façon dont nous avons obtenu l’équation d’état de Van der Waals montre qu’elle se substitue
à celle des gaz parfaits quand celle-ci n’est plus valable, c’est à dire aux fortes pressions. En effet,
lorsque la pression augmente, le volume diminue, et le covolume n’est plus négligeable devant le
volume. De plus, la distance entre molécules diminue ce qui rend leurs interactions ainsi que la
pression interne non négligeables.
Chapitre V : Les gaz, Partie C
page 5/9
(Au contraire, un gaz réel pourra être considéré comme parfait quand les dimensions des
molécules seront très petites devant les dimensions du récipient car alors les molécules
apparaîtront comme ponctuelles. Il faut aussi qu’il y ait peu de molécules par unité de volume
car alors elles seront en moyenne à grande distance les unes des autres et ainsi leurs
interactions seront négligeables.)
ii. De plus lorsqu’on comprime et refroidit un gaz parfait, son équation d’état ne prévoit pas la
liquéfaction du gaz. Au contraire, l’équation d’état de Van der Waals permet une description du
passage de l’état gazeux à l’état liquide. Voir le chapitre sur les changements d’état.
Mais cette équation ne décrit pas exactement un gaz réel. On dispose d’autres équations d’état.
c) Autres équations d’état
Lorsque les écarts entre gaz réel et gaz de Van der Waals sont trop importants pour la précision
exigée, on peut utiliser d’autres équations d’état. (Voir Complément V.2 : Quelques autres
équations d’état.)
On dispose aussi du développement du viriel2. C’est un développement en série du produit
pVm=pV/n en puissances de l’inverse du volume molaire 1/Vm=n/V :
p


V
nB n 2C n3 D
 R T  A
 2  3  ... 
n
V
V
V


A, B, C, D… sont les coefficients du viriel, fonctions de la température et de la nature du gaz. Aux
grands volumes le développement doit tendre vers l’équation d’état du gaz parfait donc A = 1.
Les autres coefficients sont déterminés expérimentalement (Voir Complément V.2) ; en théorie
ils peuvent aussi être calculés.
Il n’est pas possible de travailler avec un nombre infini de termes. On utilise donc un
développement limité, nouvelle équation d’état d’un gaz. Du nombre de termes choisis dépend la
qualité de l’accord entre le nouveau modèle et le gaz réel.
Ce développement en série se fait aussi en puissances de la pression p :
p
V
 R T ( A ' B ' p  C ' p 2  D ' p 3  ...)
n
A’, B’, C’, D’… sont de nouveaux coefficients du viriel, fonctions de la température et de la nature
du gaz. Aux faibles pressions le modèle doit tendre vers celui du gaz parfait donc A’ = 1. Ces
nouveaux coefficients du viriel s’expriment en fonction des précédents. Par exemple :
B' 
2
B
RT
et C ' 
C  B2
R 2T 2
Le mot « viriel » vient de du latin « vires » qui signifie les forces. Ce sont des considérations sur les forces
entre molécules qui permettent de calculer les coefficients du viriel.
Chapitre V : Les gaz, Partie C
page 6/9
Nous allons maintenant chercher à comparer quantitativement les comportements d’un gaz
parfait et d’un gaz de Van der Waals. Pour cela nous allons les visualiser grâce à des réseaux
d’isothermes. Nous commençons par définir ces réseaux puis nous traiterons deux exemples
souvent utilisés.
B. Isothermes, réseaux d’isothermes
1. Définitions
Une isotherme est la représentation graphique d’une variable d’état y en fonction d’une autre x
lorsque la température T est choisie constante.
L’ensemble des isothermes y = fT(x), tracées pour différentes valeurs de la température, forment
un réseau d’isothermes.
2. Exemple 1 : Diagramme de Clapeyron
Dans un diagramme de Clapeyron, on représente la pression p en fonction du volume V.
a) Cas du gaz parfait
Nous allons construire le réseau d’isothermes de Clapeyron pour un gaz parfait. La fonction
p=fT(V) que représente l’isotherme s’écrit facilement :
p
nRT C (T )

V
V
Lorsque la température T est constante, cette expression est de la forme y=constante/x. Donc sa
représentation graphique est une branche d’hyperbole.
La constante dépend de la température donc à chaque température correspond une branche
d’hyperbole. L’ensemble de ces branches d’hyperboles forme le réseau d’isothermes de
Clapeyron pour le gaz parfait.
Plus la température est élevée et plus la constante C(T) = nRT l’est. Et plus l’isotherme s’éloigne
de l’axe des abscisses. Voir figure 2, § c.
b) Cas du gaz de Van der Waals
Pour un gaz de Van der Waals, la fonction p=fT(V) s’écrit presque aussi facilement :

n2 a 
p


 V  nb   nRT
V2 

n2a
nRT
p 2 
V
V  nb
nRT
n2a
p
 2
V  nb V
C (T ) n 2 a
p

V  nb V 2
Chapitre V : Les gaz, Partie C
page 7/9
La représentation graphique de cette fonction n’est plus une branche d’hyperbole, mais il est
difficile de l’en distinguer visuellement si on ne présente pas les deux courbes simultanément.
Voici les deux réseaux, tracés grâce à Maple®.
c) Les deux réseaux de Clapeyron
Pour réaliser ces graphiques, il faut choisir une certaine quantité de gaz. Les réseaux sont tracés
pour n = 1 mol. Ce choix ne diminue pas la généralité des résultats : Il ne modifie pas la forme
des isothermes ; Il fixe l’échelle sur l’axe des abscisses car le volume, dans des conditions fixées
de température et de pression, est proportionnel à la quantité de matière.
Le réseau d’isothermes d’un gaz de Van der Waals dépend de la nature du gaz à cause des
paramètres a et b. J’ai choisi le dioxygène. Ses isothermes sont représentées en traits pleins.
Par définition, le réseau d’isothermes du gaz parfait ne dépend pas de la nature du gaz. Ces
isothermes sont représentées en traits pointillés.
Les couleurs des isothermes respectent la « convention robinetterie » : elles vont du bleu au
rouge lorsque la température augmente. Les températures s’échelonnent de 100 en 100 K entre
200 et 700 K.
pression en 105 Pa
volume en L
Figure 2 : Isothermes de Clapeyron ; en pointillés, le gaz parfait ; en pleins, O2 de Van der Waals
Nous constatons graphiquement que les écarts entre gaz de Van der Waals et gaz parfait sont
toujours faibles aux basses pressions. En effet, le comportement des gaz réels tend vers celui du
gaz parfait lorsque la pression tend vers zéro. Les écarts dépendent aussi de la température. (Et
bien entendu de la nature du gaz puisque le covolume et la pression interne en dépendent. Voir
complément V.3.)
Chapitre V : Les gaz, Partie C
page 8/9
3. Exemple n°2 : Diagramme d’Amagat
Il peut être plus démonstratif de visualiser le comportement des gaz dans un diagramme
d’Amagat, c'est-à-dire de représenter la variable y=pV en fonction de la pression p.
a) Les deux réseaux d’Amagat
Voici les deux réseaux, tracés grâce à Maple®. Nous allons ensuite décrire comment nous les
avons obtenus.
Les réseaux sont tracés pour n = 1 mol. Comme pour les réseaux de Clapeyron, ce choix ne
diminue pas la généralité des résultats. Cette fois il fixe l’échelle des ordonnées.
Le gaz choisi est encore le dioxygène. La convention des couleurs est la même et celle des traits
pleins et pointillés aussi.
pression x volume en 105 Pa.L
pression en 105 Pa
Figure 3 : Isothermes d’Amagat ; en pointillés, le gaz parfait ; en pleins, O2 de Van der Waals
b) Cas du gaz parfait
Dans ce diagramme, les isothermes du gaz parfait sont des droites parallèles à l’axe des
abscisses. En effet :
pV  nRT
y  C (T )
Cela rend la comparaison entre le gaz parfait et un gaz de Van der Waals plus aisée ce qui justifie
le choix du diagramme d’Amagat.
Chapitre V : Les gaz, Partie C
page 9/9
c) Cas du gaz de Van der Waals
Dans ce diagramme, il faut établir l’expression des isothermes. Nous avons posé y=pV et nous
remplaçons V par y/p dans l’équation de Van der Waals :

n2 a 
p


 (V  nb)  nRT
V2 



n2 a p 2  y
p


  nb   C (T )
2
y  p


Cette expression définit implicitement y=pV en fonction de p. En effet lorsqu’on se donne une
valeur numérique de la pression, l’expression ci-dessus devient une équation algébrique dont
l’inconnue est y=pV. C’est une équation du troisième degré qu’il est possible de résoudre.
d) Comparaison entre gaz parfait et gaz de Van der Waals
Le graphique ci-dessus illustre visuellement les mêmes résultats que le diagramme de Clapeyron
mais les comparaisons sont plus aisées à cause de la forme très simple des isothermes du gaz
parfait.
Dans le domaine de température et de pression représenté ici, le plus grand écart positif est
obtenu pour p = 200. 105 Pa et T = 700 K ; il vaut environ 2.105 Pa.L. Voir figure 3.
Considérons une mole de dioxygène à la température de 700 K et faisons lui subir une
compression isotherme de la pression de 105 Pa à celle de 200. 105 Pa. Le volume initial du gaz
est pratiquement le même qu’on le considère comme un gaz parfait ou comme un gaz de Van der
Waals. (Les produits pV sont pratiquement égaux sous la pression de 105 Pa. Voir figure 3.) Son
volume final est plus grand dans le cas du gaz de Van der Waals que dans celui du gaz parfait. Le
dioxygène de Van der Waals est donc moins compressible que le gaz parfait.
Dans le même domaine, le plus grand écart négatif est obtenu pour p = 200. 105 Pa et T = 200 K
et vaut environ -4.105 Pa.L. Dans ce cas le dioxygène de Van der Waals est plus compressible que
le gaz parfait.
Voir dans le complément V.3 :
- l’allure du réseau pour des gammes plus grandes de température et de pression.
- le calcul des écarts relatifs de volume à partir des écarts sur le produit pV.
- les réseaux de l’hélium, du diazote et du dioxyde de carbone.
L’équation d’état de Van der Waals, obtenue par des considérations théoriques, permet une
meilleure description du comportement des gaz, en particulier aux fortes pressions et une approche
nouvelle de leur liquéfaction.
Dans le chapitre suivant, nous continuons l’étude des gaz en étudiant quelques-unes de leurs
propriétés d’un point de vue microscopique (répartition des molécules, vitesse, énergie, notion de
température et de pression).