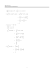MATH 141 Fundamental Theorem of Calculus (FTC) Let f : [a, b] → R

MATH 141
Fundamental Theorem of Calculus (FTC)
Let f : [a, b] → R be a continuous function.
Let F : [a, b] → R be an antiderivative of f (recall, this means F 0 (x) = f (x)).
Let x ∈ (a, b). Then :
Z
Z
b
a
f (x) dx ≡
and
a
·Z
Dx
b
F 0 (x) dx = F (b) − F (a)
¸
x
f (t)dt
= f (x) .
a
Basic Differentiation Rules
If the functions y = f (x) and y = g(x) are differentiable at x and a and b are constants, then:
1. Dx [af (x) + bg(x)] = af 0 (x) + bg 0 (x)
2. Dx [f (x) · g(x)] = f 0 (x) · g(x) + f (x) · g 0 (x)
h
3. Dx
f (x)
g(x)
i
4. Dx [f (x)]
=
r
f 0 (x) · g(x) − f (x) · g 0 (x)
[g(x)]2
r−1
= r [f (x)]
provided
g(x) 6= 0
f 0 (x)
If f is differentiable at x and g is differentiable at f (x), then:
5. Dx [g(f (x))] = g 0 (f (x)) f 0 (x)
Exp and Log
derivatives
Dx ax = ax ln a
1
Dx loga |x| =
x ln a
(loga b)(logb c) = loga c
FTC
=⇒
integrals
Z
Z
ax dx =
ax
+ C
ln a
1
dx = ln |x| + C
x
ln x
loga x =
ln a
Trig
tan x =
sin x
cos x
cot x =
cos x
sin x
sec x =
1 − cos(2x)
2
1 + cos(2x)
cos2 x =
2
sin2 x =
1
cos x
csc x =
1
sin x
sin(2x) = 2 sin x cos x
cos(2x) = cos2 x − sin2 x
FTC
=⇒
derivatives
Z
du
dx
du
Dx tan u = sec2 u
dx
integrals
cos u du = sin u + C
Dx sin u = cos u
Z
sec2 u du = tan u + C
Z
du
Dx sec u = sec u tan u
dx
du
Dx cos u = − sin u
dx
du
Dx cot u = − csc2 u
dx
du
Dx csc u = − csc u cot u
dx
sec u tan u du = sec u + C
Z
Z
Z
sin u du = − cos u + C
csc2 u du = − cot u + C
csc u cot u du = − csc u + C
more integrals
Z
tan u du
=
− ln |cos u| + C
=
ln |sec u| + C
cot u du
=
ln |sin u| + C
=
− ln |csc u| + C
sec u du
=
ln |sec u + tan u| + C
=
e
− ln |sec u − tan u| + C
csc u du
=
− ln |csc u + cot u| + C
=
e
ln |csc u − cot u| + C
Z
Z
Z
2
inverse trig functions
y = sin θ
⇔
θ = sin−1 y
where
−1≤y ≤1
and
y = cos θ
⇔
θ = cos−1 y
where
−1≤y ≤1
and
y = tan θ
⇔
θ = tan−1 y
where
y∈R
and
y = cot θ
⇔
θ = cot−1 y
where
y∈R
and
y = sec θ
⇔
θ = sec−1 y
where
|y| ≥ 1
and
y = csc θ
⇔
θ = csc−1 y
where
|y| ≥ 1
and
FTC
=⇒
derivatives
1
du
1 − u2 dx
du
1
Dx tan−1 u =
2
1 + u dx
1
du
√
Dx sec−1 u =
2
|u| u − 1 dx
−1
du
Dx cos−1 u = √
1 − u2 dx
−1 du
Dx cot−1 u =
1 + u2 dx
−1
du
√
Dx csc−1 u =
|u| u2 − 1 dx
Dx sin−1 u = √
|u| ≤ 1
|u| ≥ 1
|u| ≤ 1
|u| ≥ 1
3
π
−π
≤θ≤
2
2
0≤θ≤π
π
−π
<θ<
2
2
0<θ<π
π
0 ≤ θ ≤ π , θ 6=
2
π
−π
≤ θ ≤ , θ 6= 0
2
2
integrals
1
√
du = sin−1 u + C
1 − u2
Z
1
du = tan−1 u + C
1 + u2
Z
1
√
du = sec−1 |u| + C
u u2 − 1
Z